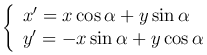Аналитическая геометрия

Уравнение линии на плоскости

Определение. Уравнением линии на плоскости (относительно выбранной системы координат) называется такое уравнение с двумя переменными

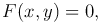
которому удовлетворяют координаты x, y любой точки данной линии и не удовлетворяют координаты ни одной точки, не лежащей на этой линии.

Здесь F(x, y) — некоторая зависимость между x и y.

Уравнение поверхности

Определение. Уравнением поверхности (в фиксированной системе координат) называется такое уравнение с тремя переменными

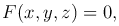
которому удовлетворяют координаты x, y, z любой точки данной поверхности и только они.

Здесь F(x, y) — некоторая зависимость между x, y и z.

Уравнение линии в пространстве

Линию в пространстве можно рассматривать как пересечение двух поверхностей, поэтому она определяется двумя уравнениями. Пусть l — линия, по которой пересекаются поверхности, определяемые уравнениями F₁(x, y, z)=0 и F₂(x, y, z)=0, то есть множество общих точек этих поверхностей, тогда координаты любой точки линии l одновременно удовлетворяют обоим уравнениям

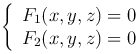
Эти уравнения и являются уравнениями указанной линии.

Например, уравнения

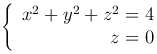
определяют окружность радиуса R=2, лежащую в плоскости Oxy. Полярные координаты

Зафиксируем на плоскости точку O и назовем ее полюсом (Рис. 1(a)). Луч [OP), исходящий из полюса, назовем полярной осью. Выберем масштаб для измерения длин отрезков и условимся, что поворот вокруг точки O против часовой стрелки будем считать положительным.

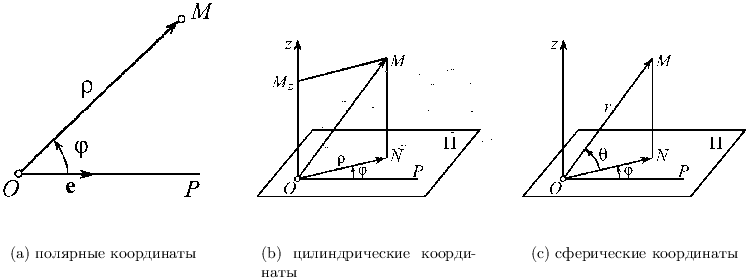
Рис. 1

Рассмотрим любую точку M на заданной плоскости, обозначим через ρ ее расстояние до полюса и назовем полярным радиусом. Угол, на который нужно повернуть полярную ось [OP), чтобы она совпадала с [OM) обозначим через φ и назовем полярным углом.

Определение. Полярными координатами точки M называются ее полярный радиус ρ и полярный угол φ.

Обозначение: M(ρ, φ).

Любой точке плоскости соответствует определенное значение ρ≥0. Значение φ для точек, отличных от точки O, определено с точностью до слагаемого 2kπ, k∈Z. Для полюса ρ=0, а φ не определено. Чтобы каждая точка плоскости получила вполне определенные значения полярных координат, достаточно считать, что 0≤φ<2π, а в полюсе φ=0. Указанные значения φ называются главными.

Рассмотрим декартову прямоугольную систему координат: полюс совпадает с началом, а полярная ось — с положительной полуосью Ox. Декартовы координаты точки M(x, y), полярные координаты точки M(ρ, φ).

Связь между прямоугольными декартовыми координатами точки и ее полярными координатами:

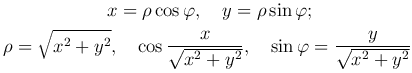
Цилиндрические и сферические координаты

В некоторой плоскости Π фиксируем точку O и исходящий из нее луч [OP) (Рис. 1(b)). Через точку O поведем прямую перпендикулярную плоскости Π и укажем на ней положительное направление; полученную ось обозначим Oz. Выберем масштаб для измерения длин. Пусть M — произвольная точка пространства, N — ее проекция на плоскость Π, M_z — проекция на Oz. Обозначим через ρ и φ полярные координаты точки N в плоскости Π относительно полюса O и полярной оси OP.

Определение. Цилиндрическими координатами точки M называются числа ρ, φ, z, где ρ, φ — полярные координаты точки N (ρ≥0, 0≤φ≤2π), а z=OM_z — величина отрезка 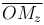оси Oz.

Запись M(ρ, φ, z) означает, что точка M имеет цилиндрические координаты ρ, φ, z. Наименование «цилиндрические координаты» объясняется тем, что координатная поверхность ρ=const является цилиндром.

Если выбрать систему прямоугольных декартовых координат, то декартовы координаты x, y, z точки M будут связаны с ее цилиндрическими координатами ρ, phi, z формулами

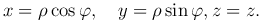
Выберем масштаб для измерения длин отрезков, зафиксируем плоскость Π с точкой O и полуосью Ox, ось Oz, перпендикулярную плоскости Π (Рис. 1(c)). Пусть M — произвольная точка пространства, N — ее проекция на плоскость Π, r — расстояние точки M до начала координат, θ — угол, образуемый отрезком 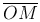с осью Oz, phi — угол, на который нужно повернуть ось Ox против часовой стрелки, чтобы она совпала с лучом ON. θ называется широтой, φ — долготой.

Определение. Сферическими координатами точки M называются числа r, θ, φ, определенные выше.

Обозначение: M(r, θ, φ).

Наименование «сферические координаты» связано с тем, что координатная поверхность r=const является сферой.

Для того, чтобы соответствие между точками пространства и тройками сферических координат (r, θ, φ) было взаимно однозначным считают, что

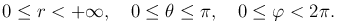
Если выбрать оси прямоугольной декартовой системы координат как на рисунке, то декартовы координаты x, y, z точки M связаны с ее сферическими координатами r, θ, φ формулами

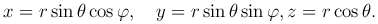
Преобразования прямоугольных координат на плоскости

а) Перенос начала или параллельный перенос.

Это означает, что при переходе от системы координат Oxy (старая) к системе координат O₁x′y′ (новая) направление осей координат остается прежним, а за новое начало координат принята точка O₁(a, b), старые координаты которой x=a, y=b. Относительно таких систем говорят, что одна получена из другой путем параллельного переноса.

Связь между старыми и новыми координатами некоторой точки M плоскости определяется следующими формулами:

старые через новые координаты: x=x′+a, y=y′+b
новые через старые координаты: x′=x-a, y′=y-b

б) Поворот координатных осей.

При этом новая сиuтема Ox′y′ получается путем поворота старой Oxy на угол α вокруг точки O против часовой стрелки. С каждой из этих координат свяжем полярную систему координат, тогда

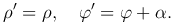
Вспоминаем формулы, выражающие координаты точки в декартовой системе через координаты точки в полярной системе

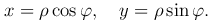
Теперь выражаем старые декартовы прямоугольные координаты x, y точки M через ее новые координаты x′, y′:

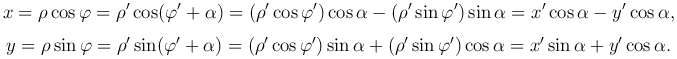
Следовательно, старые через новые координаты выражаются следующим образом:

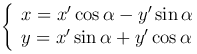
Для того, чтобы выразить x′, y′ через x, y можно поступить следующим образом. Считаем систему Ox′y′ старой, тогда переход к новой системе Oxy совершается поворотом на угол (-α), поэтому в формулах достаточно поменять местами x→x′, y→y′, записать (-α) вместо α, тогда имеем формулы, выражающие новые координаты через старые: