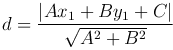Различные виды уравнения прямой на плоскости

Уравнение прямой, параллельной оси Oy декартовой системы координат:

x=a,

где a — расстояние между началом координат и точкой пересечения прямой с осью Ox.

Если a=0, то прямая совпадает с осью Oy. Ее уравнение

x=0.

Рассмотрим прямую не параллельную оси Oy, то есть прямую пересекающую ось Oy.

Уравнение прямой с угловым коэффициентом

y=kx+b,

где k — угловой коэффициент, определяемый формулой

k=tg α,

α — угол, между прямой и осью Ox, b=OB — величина направленного отрезка 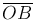, отсекаемого прямой на оси Oy (рис. 1).

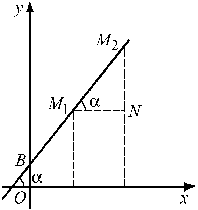
рис. 1

Если прямая параллельна оси Ox, то есть α=0, k=0, то это уравнение примет вид

y=b.

Ось Ox определяется уравнением

y=0.

Угловой коэффициент k прямой выражается через координаты двух различных точек M₁(x₁, y₁), M₂(x₂, y₂), принадлежащей прямой, следующим образом

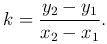
Геометрический смысл: Это равенство определяет тангенс угла M₁ в прямоугольном треугольнике M₁M₂N.

Пусть заданы угловой коэффициент k прямой и ее точка M₁(x₁, y₁). Тогда

y-y₁=k(x-x₁)

— уравнение прямой, проходящей через данную точку в данном направлении.

Уравнение прямой, проходящей через две данные точки M₁(x₁, y₁), M₂(x₂, y₂):

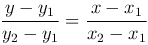
Параметрические уравнения прямой:

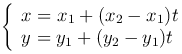
где t — параметр. При t=0 получаем координаты точки M₁(x₁, y₁), при t=1 — координаты точки M₂(x₂, y₂), при 0<t<1 — координаты любой точки, принадлежащей (M₁, M₂). Когда t∈(-∞, +∞), то точка M(x,y) описывает рассматриваемую прямую.

Пусть прямая отсекает на координатных осях отрезки, величины которых равны соответственно a и b. Тогда уравнение

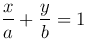
является уравнением прямой в отрезках.

Рассмотрим общее уравнение первой степени относительно прямоугольных декартовых координат x, y

Ax+By+C=0, где A²+B²≠0.

Теорема. Каждое уравнение первой степени относительно декартовых координат определяет прямую. Обратно, каждая прямая на плоскости в фиксированной декартовой прямоугольной системе координат определяется уравнением первой степени.

Теорема означает, что линии первого порядка это прямые. Уравнение:

Ax+By+C=0

— общее уравнение прямой.

Формула k=-A/B определяет угловой коэффициент этой прямой, если B ≠ 0. Если B=0, то уравнение примет вид x=a (a=-C/A) и определяет прямую, параллельную оси Oy ($α=π/2, tg α=∞); такая прямая не имеет углового коэффициента.

Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых

Рассмотрим две прямые l₁, l₂. Предположим, что ни одна из них не параллельна оси Oy.

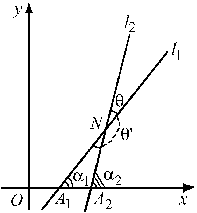
Рис. 2

Обозначим через θ угол наклона второй прямой к первой, то есть угол на который нужно повернуть вокруг точки пересечения прямую l₁, чтобы она совпала с l₂.

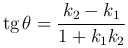
— формула тангенса угла между двумя прямыми.

Замечание 1. При другой нумерации прямых (k₁↔k₂) правая часть последней формулы меняет знак. Тогда эта формула определяет тангенс угла θ′ между двумя прямыми, причем θ+θ′=π.

Замечание 2. Острый угол между двумя прямыми можно находить по формуле

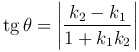
Если одна из прямых, например, l₂ параллельная оси Oy, то угол θ находится непосредственно: α₂=π/2, следовательно, θ=π/2-α₁.

Необходимое и достаточное условие параллельности прямых:

k₁=k₂.

Необходимое и достаточное условие перпендикулярности прямых: Угловые коэффициенты перпендикулярных прямых обратны по величине и противоположны по знаку, то есть

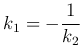
Если прямые заданы общими уравнениями:

A₁x+B₁y+C₁=0
A₂x+B₂y+C₂=0,

то тангенс угла между ними определяется формулой

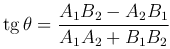
(угловые коэффициенты здесь k₁=-A₁/B₁, k₂=-A-2/B-2).

Необходимое и достаточное условие параллельности прямых:

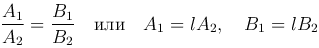
Необходимое и достаточное условие перпендикулярности прямых:

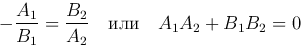
Отметим, что прямые, заданные уравнениями

Ax+By+C=0, Bx-Ay+C=0

взаимно перпендикулярны, так как для них выполнено необходимое и достаточное условие.

Расстояние от точки до прямой

Дана прямая l: Ax+By+C=0 и точка M₁(x₁, y₁) относительно прямоугольной декартовой системы координат. Расстояние от этой дочки до прямой вычисляется по формуле