Корпускулярно-волновой дуализм

Из опытных фактов следует, что при взаимодействии с веществом свет обнаруживает корпускулярные свойства. Однако представление о свете как потоке классических корпускул несовместимо с классическими представлениями об электромагнитных волнах (которые подтверждаются в явлениях интерференции и дифракции).

Очевидно явное противоречие. Действительно, соотношения для энергии и импульса фотона (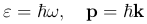) связывают корпускулярные и волновые свойства света: левые части (ε и р) характеризуют фотон как частицу, правые же содержат ω и k, что определяет их волновые свойства. Но именно сосуществование этих свойств и не может быть логически непротиворечиво объяснено классической физикой. С точки зрения последней понятия частицы и волны исключают друг друга. Каким образом фотон-частица может иметь волновые свойства?

Представить себе такой объект, который совмещал бы несовместимое, - это выше возможностей нашего (классического) воображения. Опытные же факты вынуждают констатировать, что это так и есть, т. е. свет обнаруживает корпускулярно волновой дуализм (двойственность). При этом фотон проявляет свои корпускулярно-волновые свойства в разных соотношениях: например, в области длинных волн - в основном волновые свойства, а в области коротких волн - корпускулярные.

Итак, фотон нельзя представить моделью, описываемой классическим образом. Он является квантовым объектом, который в принципе невозможно представить себе с помощью классических образов. Мы вынуждены признать, что при изучении явлений следует руководствоваться не тем, что доступно нашему воображению, а тем, что дают наблюдения и опыт.

Забегая вперед, отметим, что обычные корпускулы - электроны, нейтроны, атомы и др., как выяснилось в дальнейшем, обладают и волновыми свойствами.

Эффект Комптона. Опыты Комптона

Комптон (1923) открыл явление, в котором можно было наблюдать, что фотону присущи энергия и импульс. Результаты этого опыта - еще одно убедительное подтверждение гипотезы Эйнштейна о квантовой природе самого электромагнитного излучения.

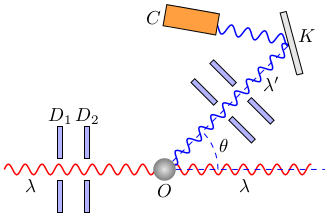
Опыт Комптона
Рис. 5

Комптон исследовал рассеяние жесткого рентгеновского излучения на образцах, состоящих из легких атомов, таких как графит, парафин и др. Схема его установки показана на рис. 5.

Источником рентгеновского излучения служила рентгеновская трубка с молибденовым антикатодом. Диафрагмы D₁ и D₂ выделяли узкий пучок монохроматического рентгеновского излучения, который падал затем на исследуемый образец О. Для исследования спектрального состава рассеянного излучения оно после прохождения ряда диафрагм попадало на кристалл К рентгеновского спектрографа, а затем в счетчик С (или на фотопластинку).

Комптон обнаружил, что в рассеянном излучении, наряду с исходной длиной волны λ , появляется смещенная линия с длиной волны λ′ > λ. Это получило название комптоноеского смещения, а само явление — эффекта Комптона.

Опыт показал, что наблюдаемое комптоновское смещение λ′ - λ, не зависит от материала рассеивающего образца и длины волны λ падающего излучения, а определяется лишь углом θ между направлениями рассеянного и падающего излучений (см. рис. 5). С увеличением угла интенсивность смещенной компоненты растет, а несмещенной - падает.

Спектральные закономерности. В первую очередь нас будут интересовать спектры, обусловленные излучением невзаимодействующих друг с другом атомов. Эти спектры состоят из отдельных узких спектральных линий, и их называют линейчатыми.

Наличие многих спектральных линий указывает на сложность внутреннего строения атома. Изучение атомных спектров послужило ключом к познанию внутренней структуры атомов. Прежде всего было замечено, что спектральные линии расположены не беспорядочно, а образуют серии линий. Изучая линейчатый спектр атомарного водорода, Бальмер (1885) установил следующую закономерность. В современных обозначениях она выглядит так;

()

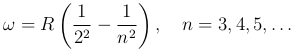где ω - циклическая частота, соответствующая каждой спектральной линии (ω = 2 π c/λ ), R - постоянная Ридберга:

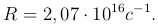
Заметим, что в спектроскопии принято характеризовать спектральные линии не частотой, а так называемым волновым числом :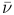

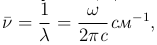
где λ - длина волны. Формула Бальмера, написанная для волнового числа 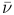, имеет такой же вид, как ():

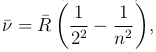
где постоянная Ридберга 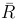имеет значение

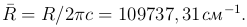
Формулу () называют формулой Бальмера, а соответствующую серию спектральных линий — серией Бальмера. Основные линии этой серии находятся в видимой части спектра. Дальнейшие исследования спектра атомарного водорода показали, что имеется еще несколько серий. В ультрафиолетовой части спектра — серия Лаймана:

()

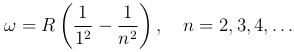а в инфракрасной части спектра — серия Пашена:

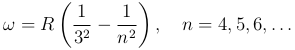
а также серии Брэкета и Пфунда.

Все эти серии можно представить в виде обобщенной формулы Бальмера:

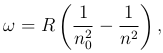
где n₀ = 1 для серии Лаймана, n₀ = 2 для серии Бальмера и т. д. При заданном n₀ число n принимает все целочисленные значения, начиная с n₀ + 1.

Максимальной длине волны серии Лаймана () отвечает n=2, это λ_max = 2 π/ω_min = 8 π с /3 R = 121,6 нм. Соответствующую спектральную линию называют резонансной линией водорода.

С ростом n частота линий в каждой серии стремится к предельному значению R/n₀², которое называют границей серии. За границей серии спектр не обрывается, а становится сплошным. Это присуще не только всем сериям водорода, но и атомам других элементов.

Таким образом, интересующая нас серия заключена в спектральном интервале от 365 до 656 нм, т. е. действительно, все основные линии ее расположены в видимой области спектра.