Понятие о краевых задачах для дифференциальных уравнений

Помимо задачи с начальными условиями или задачи Коши в приложениях встречается и другая постановка задачи - значение искомой функции задается не в одной, а в двух точках, ограничивающих отрезок, на котором требуется определить решение. Такая задача называется краевой или граничной.

Например, в задаче о движении материальной точки массы m под действием заданной силы 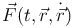часто требуется найти закон движения, если в начальный момент t = t₀ точка находилась в положении, характеризуемом радиус-вектором 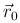, а в момент t = t₁ должна попасть в точку 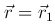. Задача сводится к интегрированию дифференциального уравнения движения

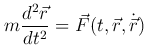
с краевыми условиями .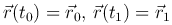

Заметим, что эта задача имеет, вообще говоря, не единственное решение. Если речь идет о баллистической задаче и о точках земной поверхности, то в одну и ту же точку тело может попасть по разным траекториям.

Рассмотрим краевые задачи для линейных уравнений второго порядка

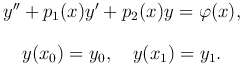
Заменой переменных

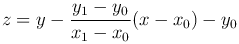
краевые условия сводятся к нулевым условиям z(x₀)=z(x₁)=0, причем линейность дифференциального уравнения не нарушается. Умножим это уравнение на exp(∫p₁(x)dx), получим

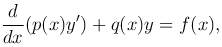
где p(x)=exp(∫p₁(x)dx). Без ограничения общности изучение исходной краевой задачи можем заменить изучением следующей краевой задачи:

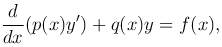(1)

с граничными условиями

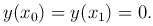(2)

Пусть функция f(x) равна нулю на всем отрезке [x₀, x₁], за исключением ε-окрестности точки x=s, s - ε < x < s + ε, причем

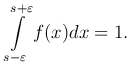
Обозначим эту функцию f(x)=f_{ε(x, s)}.

Определение. Функцией Грина G(x, s) краевой задачи (1), (2) называется функция, удовлетворяющая следующим условиям:

1) G(x, s) непрерывна по x при фиксированном s при x₀ ≤ x ≤ x₁, x₀ ≤ s ≤ x₁;
2) G(x, s) является решением соответствующего однородного уравнения

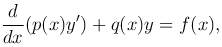
на всем отрезке [x₀, x₁], за исключением точки x = s;
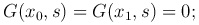
3) G(x, s) удовлетворяет граничным условиям:
4) В точке x = s производная G′_x(x, s) должна иметь разрыв первого рода со скачком 1/p(s).

Функция

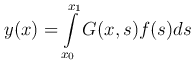
является решением уравнения (1). Краевые условия (2) удовлетворяются по 2 свойству. Метод построения функции Грина. Рассмотрим решение y₁(x) уравнения

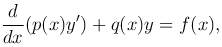
определяемое начальными условиями

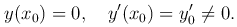
Это решение, вообще говоря, не удовлетворяет второму граничному условию y(x₁)=0. Предполагаем, что не существует нетривиального решения y(x) этого однородного уравнения, удовлетворяющего нулевым граничным условиям y(x₀)=y(x₁)=0.

Очевидно, что решения C₁y₁(x), где C₁ — произвольная постоянная, также удовлетворяет граничному условию y(x₀)=0. Аналогично находим нетривиальное решение y₂(x) однородного уравнения, удовлетворяющее второму граничному условию y₂(x₁)=0. Этому же условию удовлетворяют все решения C₂y₂(x), где C₂ — произвольная постоянная.

Функцию Грина ищем в виде

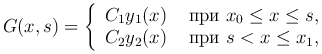
причем постоянные C₁, C₂ выберем так, чтобы были выполнены свойства 1) и 4), то есть, чтобы функция G(x, s) была непрерывна по x при фиксированном s, и, в частности, непрерывна в точке x=s:

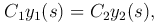
и чтобы G′_x(x, s) в точке x=s имела скачок l/p(s):

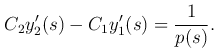
В силу предположения, что y₁(x₁) ≤ 0, решения y₁(x) и y₂(x) линейно независимы, так как все линейно зависимые от y₁(x) решения имеют вид C₁y₁(x) и, следовательно, при C₁ ≠ 0 не обращаются в нуль в точке x₁, в которой обращается в нуль решение y₂(x). Следовательно, определитель системы

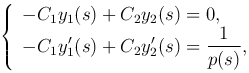
являющийся определителем Вронского: W(y₁(x), y₂(x))=W(x) в точке x=s, отличен от нуля и постоянные C₁ и C₂, удовлетворяющие этой системе, легко определяются:

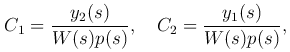
откуда