Дифференциальные уравнения
Дифференциальные уравнения
 Комплексные числа
Комплексные числа
Определение. Комплексным числом называется упорядоченная пара (x, y) вещественных чисел, первое из которых называется действительной частью, а второе — мнимой частью этого комплексного числа.
В случае, когда мнимая часть y равна нулю, соответствующую пару (x, 0) договариваются отождествлять с вещественным числом x. Это позволяет рассматривать множество всех вещественных чисел как часть множества комплексных чисел.
Определение. Два комплексных числа z1=(x1, y1) и z2=(x2, y2) называются равными, если x1=x2, y1=y2. Говорят, что комплексное число z=(x, y) равно нулю, если x=0, y=0.
Определим операции сложения и умножения комплексных чисел.
Определение. z1=(x1, y1) и z2=(x2, y2) назовем комплексное число z вида
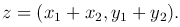
Произведением двух комплексных чисел z1=(x1, y1) и z2=(x2, y2) назовем комплексное число z вида
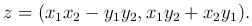
Сумма и произведение комплексных чисел обладают теми же самыми свойствами, что и сумма и произведение вещественных чисел.
Свойства:
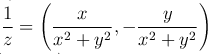 такое, что
такое, что 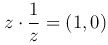 .
.
Определение. Разностью двух комплексных чисел z1=(x1, y1) и z2=(x2, y2) называется такое комплексное число z, которое в сумме с z2 дает z1.
Легко проверить, что разность двух комплексных чисел определяется по формуле:
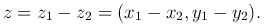
Определение. Частным двух комплексных чисел z1=(x1, y1) и z2=(x2, y2)≠0 называется такое комплексное число z, которое при умножении на z2 дает z1.
Легко проверить, что частное двух комплексных чисел определяется по формуле:
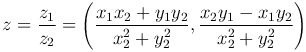
В операциях с комплексными числами особую роль играет число, представимое парой (0, 1) и обозначаемое буквой i. Найдем
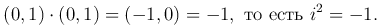
Тогда любое комплексное число z=(x, y) можно представить в виде
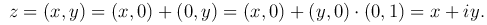
Таким образом получили
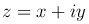
— алгебраическая форма записи комплексного числа. Число x называется действительной частью (Re z), число y называется мнимой частью (Im z) этого комплексного числа.
Два комплексных числа z1=x1+i y1 и z2=x2+i y2 равны тогда и только тогда, когда x1 = x2 и y1 = y2.
Замечание 1. Одно равенство z1=z2 комплексных чисел равносильно двум равенствам x1 = x2, y1 = y2 действительных чисел.
Замечание 2. Понятия «больше», «меньше» для комплексных чисел не определяется. Записи типа i>0, 1+i<2 лишены всякого смысла.
Определение. Комплексные числа x+iy и x-iy, то есть числа, отличающиеся только знаком мнимой части, называются сопряженными.
Число, сопряженное числу z, обозначается 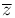 .
.
На плоскости выберем систему прямоугольных координат. Комплексному числу (a, b)=a+bi поставим в соответствие точку M(a, b) этой плоскости.
Если b=0, то получим действительное число (a, 0)=a, которое изображается точкой A на оси Ox, поэтому ось Ox называется действительной осью.
Если a=0, то получим чисто мнимое число (0, b)=bi, которое изображается точкой B на оси Oy, поэтому ось Oy называется мнимой осью.
Мнимая единица i изображается точкой (0, 1).
Любое комплексное число z=(a, b), где a≠0, b≠0 изображается точкой плоскости, не лежащей на осях координат. Обратно, любой точке плоскости M(a, b) соответствует комплексное число (a, b)=a+bi. Таким образом, между множеством комплексных чисел и множеством точек плоскости установлено взаимно-однозначное соответствие.
Определение. Плоскость, точки которой отождествлены с комплексными числами, называется комплексной плоскостью.
Определение. Модулем комплексного числа z=a+bi называется длина отрезка 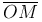 , где O — начало координат, M(a, b) — точка, изображающая это комплексное число.
Обозначение: r, |z|.
Таким образом,
, где O — начало координат, M(a, b) — точка, изображающая это комплексное число.
Обозначение: r, |z|.
Таким образом, 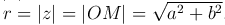 , следовательно,
, следовательно,
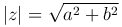
— формула, выражающая модуль комплексного числа через его действительную и мнимую части.
Определение. Аргументом комплексного числа z=a+bi называется величина угла φ наклона отрезка OM к оси Ox.
Аргумент комплексного числа z имеет бесконечное множество значений, отличающихся на число, кратное 2π. Аргумент не определен лишь для z=0, для которого |z|=0.
Обозначение: Arg z.
Выделяют главное значение аргумента, для которого -π≤φ≤&pi. Обозначение: arg z.
Поскольку a=r cos φ, b=r sin φ, то
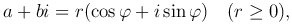
где
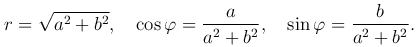
Определение. r(cos φ+i sin φ) называется тригонометрической формой комплексного числа.
Два комплексных числа, заданных в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на величину, кратную 2π, то есть
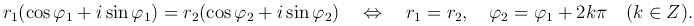
С помощью формулы Эйлера
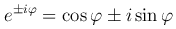
тригонометрическая форма комплексного числа преобразуется в показательную форму комплексного числа:
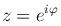
Рассмотрим два комплексных числа:

Найдем произведение этих комплексных чисел:
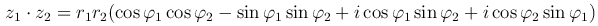
или
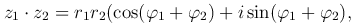
следовательно,
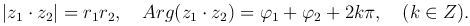
В показательной форме получим
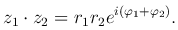
Если z2≠0, r2≠0, то
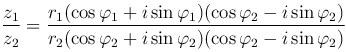
и это выражение преобразуется к виду
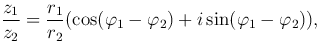
следовательно,
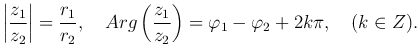
В показательной форме получим
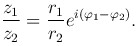
Рассмотрим комплексное число z=r(cos φ+i sin φ). Пусть n∈N, тогда
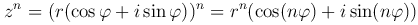
— формула Муавра.
Определение. Комплексное число z называется корнем степени n из комплексного числа w, если zn=w.
Обозначение: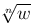 .
.
Пусть z=r(cos φ+i sin φ), w=ρ(cos α+i sin α). Поскольку zn=w, то по формуле Муавра получим
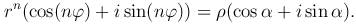
Из равенства двух комплексных чисел получим
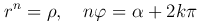
или
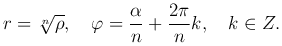
Итак, все решения уравнения zn=w представляются в виде
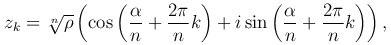
причем при k=1, 2, …, n-1 получаем различные значения корня.
Таким образом, существует n корней степени n из числа w. Все эти корни имеют один и тот же модуль, но разные аргументы, отличающиеся друг от друга на 2πk/n, где k — некоторое целое число.
В показательной форме