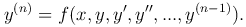Дифференциальные уравнения

Определение. Дифференциальным уравнением называется уравнение относительно неизвестной функции (или вектор-функции) и ее производных или дифференциалов различных порядков. Порядком дифференциального уравнения называется порядок старшей производной или дифференциала, входящей в это уравнение.

Примеры дифференциальных уравнений:

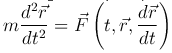1. — ускорение движения точки массы m под влиянием силы 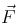, зависящей от времени, положения точки, определяемого радиус-вектором 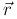, и ее скорости 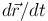. Сила равна произведению массы на ускорение. Это дифференциальное уравнение второго порядка.
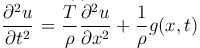2. — уравнение колебания струны, закрепленной на концах, отклонение которой от положения равновесия u=u(x,t), с постоянной величиной натяжения T и линейной плотностью ρ, на которую воздействуют внешние силы, плотность распределения которых равна g(x,t).

Основной задачей теории дифференциальных уравнений является нахождение неизвестных функций, определяемых дифференциальными уравнениями.

Если искомая функция зависит от одной переменной, то соответствующее дифференциальное уравнение называется обыкновенным. Если же искомая функция зависит от нескольких переменных, то соответствующее дифференциальное уравнение называется уравнением с частными производными.

Общий вид обыкновенного дифференциального уравнения n-го порядка:

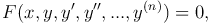
где x — независимая переменная; y=y(x) — искомая функция переменной x; y′, y″, …, y⁽ⁿ⁾ — ее производные; F(x, y, y′, y″, …, y⁽ⁿ⁾) — заданная функция своих аргументов. Функция F может не содержать некоторых своих аргументов, но обязательно должна зависеть от y⁽ⁿ⁾.

Если это уравнение разрешимо относительно производной n-го порядка, то его можно представить в виде