Дифференциальные уравнения первого порядка

Дифференциальные уравнение первого порядка в общем виде записывается следующим образом:

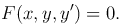(1)

Если это уравнение разрешимо относительно y′, то

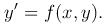(2)

Пользуясь другим обозначением производной, можем записать это уравнение в виде

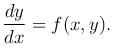
Функция y=φ(x), определенная и непрерывно дифференцируемая в интервале (a, b), называется решением дифференциального уравнения (1) или (2) в этом интервале, если она обращает это уравнение в тождество, т.е.

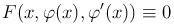
для всех x∈(a, b). Сама задача нахождения решений дифференциального уравнения называется обычно задачей интегрирования дифференциального уравнения.

В простейшем случае, когда правая часть уравнения (2) не содержит y, получается дифференциальное уравнение вида

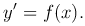
Нахождение его решений есть основная задача интегрального исчисления, и все множество этих решений дается формулой

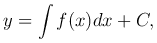
где C — произвольная постоянная. Таким образом, в этом простейшем случае имеется семейство решений дифференциального уравнения, содержащее произвольную постоянную. Как мы увидим, и в общем случае дифференциального уравнения первого порядка получается семейство решений, содержащее произвольную постоянную:

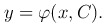
Такое семейство решений называется общим интегралом уравнения. Общий интеграл может выражаться в неявной форме или в форме, решенной относительно C:

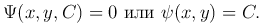
Придавая произвольной постоянной C различные численные значения, будем получать различные частные решения уравнения.

Геометрическая интерпретация дифференциального уравнения и его решений

Если рассматривать x и y как как координаты точек плоскости, то дифференциальное уравнение (2) определяет в каждой точке (x, y), где определена функция f(x, y) угловой коэффициент касательной y′ к некоторой линии. Искомое решение y=φ(x) уравнения (2) есть такая кривая, которая в каждой своей точке имеет угловой коэффициент касательной y′, определяемый равенством (2). Такая кривая называется интегральной кривой (или интегральной линией) дифференциального уравнения. Т.е. понятие решения уравнения (2) совпадает с понятием интегральной кривой этого уравнения на плоскости Oxy. Общий интеграл y=φ(x, C) дает бесчисленное множество интегральных кривых (семейство кривых, зависящее от одной произвольной постоянной).

Задача Коши для дифференциального уравнения первого порядка: найти решение y=φ(x) уравнения (1), удовлетворяющее условию

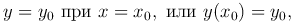
где x₀, y₀ — заданные числа. Геометрически задача Коши означает следующее: найти интегральную линию, проходящую через точку M₀(x₀,y₀).

Если известно общее решение y=φ(x, C) уравнения y′=f(x, y) или его общий интеграл Φ(x, y, C)=0, то нахождение решения задачи Коши сводится к вычислению значения произвольной постоянной C из уравнения y₀=φ(x₀, C) или уравнения Φ(x₀, y₀, C)=0.

Методы решения дифференциальных уравнений бывают точные, приближенные и численные. Точные методы дают решение, которое можно выразить через элементарные функции. Получить точное решение дифференциального уравнения можно не всегда. Например, решение уравнения y′=x²+y² не выражается через элементарные функции. Приближенные методы дают решение в виде некоторой последовательности функций y_m(x) , сходящейся к решению y(x) при m→∞. Численные методы дают решение в виде таблицы значений функции y(x).