Однородные дифференциальные уравнения первого порядка

Определение. Функция F(x, y) называется однородной измерения n, если при любом t выполняется тождество

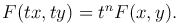
Примеры однородных функций первого, второго и нулевого измерений соответственно:

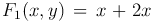
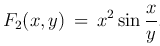
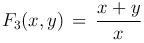
Определение. Дифференциальное уравнение первого порядка называется однородным, если P(x, y) и Q(x, y) — однородные функции одного и того же измерения n.

В этом случае имеем

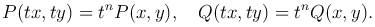
Полагая в последних равенствах t = 1/x, x≠0, получаем

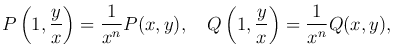
откуда

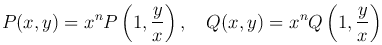
Подставив эти выражения в уравнение

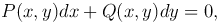
получим

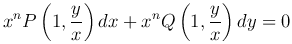
или

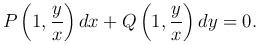
Введем новую переменную u по формуле

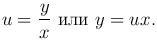
Поскольку в этом случае dy = udx + xdu, то придем к уравнению

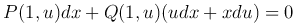
или

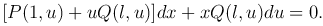
Это уравнение является уравнением с разделяющимися переменными x, u; из него определяется u, а потом — искомая функция y = ux. Если Φ(x, u, c) = 0 — общий интеграл этого уравнения с разделяющимися переменными, то Φ(x, y/x ,c) = 0 — общий интеграл однородного уравнения P(x,y)dx+Q(x,y)dy=0.

Уравнение не содержит искомой функции и ее производных до порядка k-1 включительно:

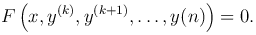
В этом случае порядок уравнения может быть снижен до n - k заменой переменной y^(k)=z. Действительно, тогда y^(k+1)=z′, y^(k+2)=z″, …, y⁽ⁿ⁾=z^(n-k) и получим уравнение

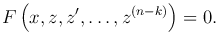
Если z = φ(x, C₁, C₂, …, C_n-k) — общее решение данного уравнения, то придем к уравнению

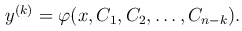
Из этого уравнения функция y находится путем интегрирования k раз.

III. Уравнение не содержит независимой переменной:

С помощью подстановки z = y′ порядок этого уравнения понижается на единицу. Действительно,

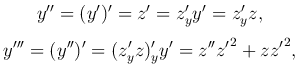
производная k-го порядка от y по x выражается через производные (k - 1)-го порядка от z по y. Итак, уравнение примет вид:

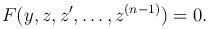
IV. Левая часть уравнения

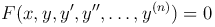
является производной некоторого дифференциального выражения (n -1)-го порядка Ψ(x, y,y′, …, y^(n-1)). Тогда это уравнение можно переписать в виде:

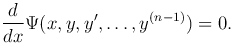
Если y = y(x) является решением последнего уравнения, то производная функции Ψ(x, y, y′, …, y^(n-1)) тождественно равна нулю. Следовательно, функция Ψ(x, y, y′, …, y^(n-1)) равна постоянной, получаем первый интеграл

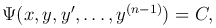
то есть дифференциальное уравнение (n -1)-го порядка, содержащее одну произвольную постоянную, эквивалентное исходному уравнению n-го порядка. Таким образом, порядок уравнения понизился на единицу.

Часто в приложения встречаются дифференциальные уравнения второго порядка, допускающие понижение порядка.

1) F(x, y″)=0.
Это уравнение можно разрешить относительно второго аргумента y″= f(x) и два раза проинтегрировать или ввести параметр t и заменить уравнение двумя параметрическими уравнениями: y″=φ(t) и x=ψ(t), откуда
2) F(y′, y″)=0.
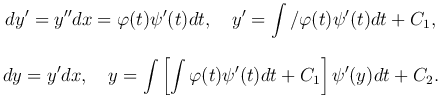
Полагая y′=z, это уравнение преобразуется к уравнению F(z, z′)=0. Если это уравнение разрешимо относительно z′, то есть z′=f(z), это есть уравнение с разделяющимися переменными. Если же это уравнение трудно разрешить относительно z′, то можно ввести параметр t и заменить его параметрическими уравнениями z=φ(t) и z′=ψ(t). Так как dy=y′dx, то

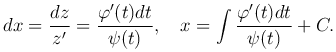
Следовательно, искомые интегральные кривые в параметрической форме определяются уравнениями
3) F(y, y″)=0.
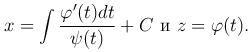
Полагая y′=z, y″=z_y′y′=zz_y′, тогда это уравнение преобразуется к уравнению F(y, zz′(y))=0. Если это уравнение разрешимо относительно второго аргумента, то есть zz′=f(y), отсюда zdz=f(y)dy — а это уравнение с разделяющимися переменными.