Линейная зависимость и линейная независимость функций

Понятие линейной независимости функций вводится аналогично понятию линейной независимости векторов.

Определение. Функции

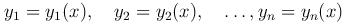
называются линейно-зависимыми на отрезке [a, b], если существуют действительные числа α₁, α₂, …, α_n, не все равные нулю (α²₁+α²₂+ … + α²_n≠0), такие, что для любых x∈[a, b] выполняется равенство

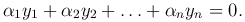
Если это равенство выполняется лишь при α₁=α₂=…=α_n=0, то функции y₁, y₂, …, y_n называются линейно-независимыми.

Примеры.

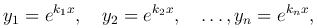
1) Функции y₁=1, y₂=x, y₃=x², …, y_n=x^n-1 линейно независимы на любом отрезке [a, b].
2) Если k_i≠k_j при i≠j, то функции

а также функции

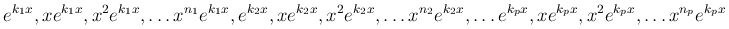
линейно независимы на любом отрезке [a, b].

Определитель Вронского

Определение. Определителем Вронского называется определитель

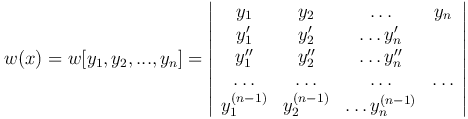
Теорема. Если функции y₁=y₁(x), y₂=y₂(x), …, y_n=y_n(x) линейно-зависимы на отрезке [a, b], то определитель Вронского w(x) = w[y₁, y₂, …, y_n] тождественно равен нулю на этом отрезке.

Теорема. Если y₁=y₁(x), y₂=y₂(x), …, y_n=y_n(x) линейно-независимые решения уравнения

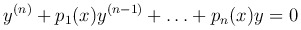
с коэффициентами p_k(x) (k=l, …, n), непрерывными на отрезке [a, b], то определитель Вронского w(x) = w[y₁, y₂, …, y_n] не обращается в нуль ни в одной точке отрезка [a, b].

Общее решение линейного однородного уравнения n-го порядка

Теорема. Если y₁=y₁(x), y₂=y₂(x), …, y_n=y_n(x) — линейно-независимые на отрезке [a, b] решения однородного уравнения

коэффициенты которого непрерывны на этом отрезке, то его общее решение определяется формулой

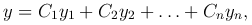
где C₁, C₂, …, C_n — произвольные постоянные.

Следствие. Максимальное число линейно-независимых решений линейного однородного уравнения равно порядку этого уравнения.

Определение. Любые n линейно-независимых решений линейного однородного уравнения n-го порядка называются его фундаментальной системой решений.