Линейные неоднородные уравнения n-го порядка

Рассмотрим линейное неоднородное уравнение n-го порядка

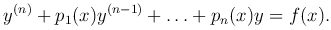
Будем считать, что функции p_k(x) (k=1, …, n) и f(x) непрерывны на отрезке [a, b]. Неоднородное уравнение кратко запишем так:

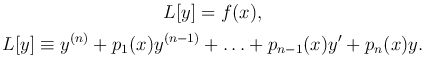
Теорема. Если y₀ — решение однородного уравнения L[y]=0, y₁ — решение соответствующего неоднородного уравнения L[y] = f(x), то сумма y₀+y₁ является решением этого неоднородного уравнения.

Структура общего решения неоднородного уравнения определяется следующей теоремой.

Теорема. Если Y — частное решение уравнения L[y] = f(x) с непрерывными коэффициентами, 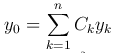— общее решение соответствующего однородного уравнения L[y] = 0, то общее решение данного неоднородного уравнения определяется формулой

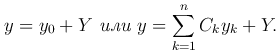
Замечание. Чтобы записать общее решение линейного неоднородного уравнения, необходимо найти какое-нибудь частное решение этого уравнения и общее решение соответствующего однородного уравнения.

Линейные неоднородные уравнения n-го порядка с постоянными коэффициентами

Рассмотрим линейное неоднородное уравнение n-го порядка с постоянными коэффициентами

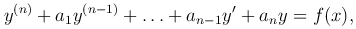
где a₁, a₂, …, a_n — действительные числа. Запишем соответствующее однородное уравнение

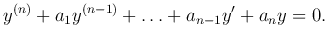
Общее решение неоднородного уравнения определяется формулой

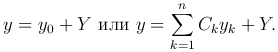
Общее решение однородного уравнения y₀ находить умеем, частное решение Y может быть найдено методом неопределенных коэффициентов в следующих простейших случаях:

1. f(x) = e^axP_n(x), где P_n(x) — многочлен степени n.
Если a не является корнем соответствующего характеристического уравнения, то полагают Y= e^axQ_n(x), где Q_n(x) — многочлен степени n с неопределенными коэффициентами.
Если a — корень характеристического уравнения, то Y=x^re^axQ_n(x), где r — кратность корня a.
2. f(x) = e^ax(P_n(x) cos bx + R_m(x) sin bx).
Если a±ib не являются корнями характеристического уравнения, то полагают

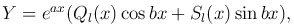
где Q_l(x), S_l(x) — многочлены степени l = max(n, m) с неопределенными коэффициентами.
Если a±ib — корни характеристического уравнения, то

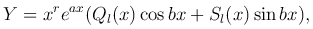
где r — кратность корней a±ib.

В общем случае применяется метод вариации произвольных постоянных.

Метод вариации произвольных постоянных

Рассмотрим линейное неоднородное уравнение n-го порядка с переменными коэффициентами

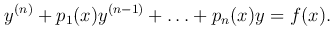
Будем считать, что функции p_k(x) (k=1, …, n) непрерывны на некотором отрезке [a, b].

Если нахождение частного решения этого уравнения оказывается затруднительным, но известно общее решение соответствующего однородного уравнения, то общее решение неоднородного уравнения можно найти методом вариации произвольных постоянных.

Пусть соответствующее однородное уравнение

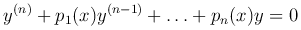
имеет общее решение

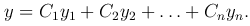
Общее решение неоднородного уравнения будем искать в виде

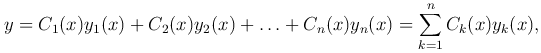
где y₁=y₁(x), y₂=y₂(x), …, y_n=y_n(x) — линейно-независимые решения однородного уравнения, входящие в его общее решение, а C₁(x), C₂(x), …, C_n(x) — неизвестные функции. Чтобы найти эти функции, подчиним их некоторым условиям.

Найдем производную

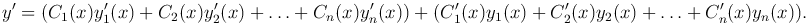
Потребуем, чтобы сумма во второй скобке равнялась нулю, то есть

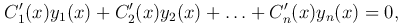
тогда

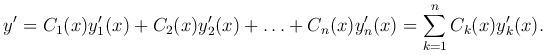
Найдем вторую производную

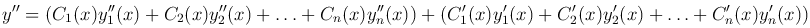
и потребуем, чтобы

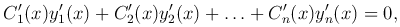
тогда

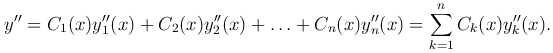
Продолжая аналогичный процесс, получим

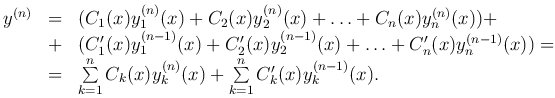
В этом случае нельзя требовать, чтобы сумма во второй скобке обратилась в нуль, так как функции C₁(x), C₂(x), …, C_n(x) уже подчинены n-1 условиям, а нужно еще удовлетворить исходному неоднородному уравнению.

Подставим в это неоднородное уравнение выражения для функции y и ее производных, получим

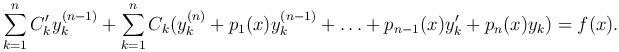
Поскольку y_k = y_k(x) (k=1, …, n) — решения однородного уравнения, то

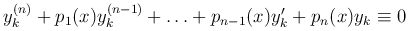
и последнее уравнение примет вид

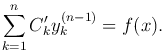
Следовательно, для определения функций C′_k(x) (k=1, …, n) имеем систему линейных уравнений

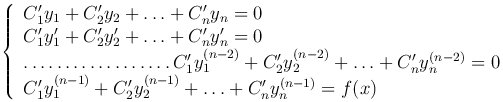
Определитель этой системы отличен от нуля, как определитель Вронского для линейно-независимых функций, поэтому система имеет единственное решение.

Из этой системы находим C′_k=φ_k(x) (k=1, …, n), а потом и сами функции

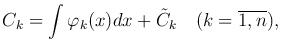
где 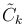— постоянные.

Подставляя эти выражения в формулу

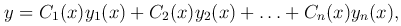
получаем искомое общее решение неоднородного уравнения.