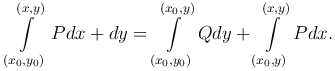Линейные дифференциальные уравнения первого порядка

Определение. Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной.

Линейное дифференциальное уравнение имеет вид

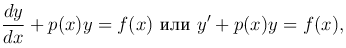
где p(x), f(x) — непрерывные на отрезке [α, β] функции.

Если f(x) ≡ 0, то это уравнение называется линейным однородным. В линейном однородном уравнении переменные разделяются 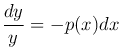. Интегрируя, получим

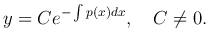
При делении на y потеряли решение y ≡ 0. Его можно включить в общее решение, если считать, что C может равняться нулю.

Таким образом, общее решение линейного однородного уравнения:

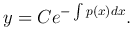
Решение неоднородного линейного уравнения (f(x) ≠ 0) ищется в виде произведения двух функций:

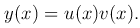
Так как y′=u′v+v′u, то u′v + [v′+p(x)v]u = f(x). В качестве v возьмем функцию, удовлетворяющую условия

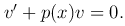
Это есть линейное однородное уравнение, его решение:

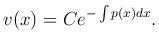
Осталось решить уравнение u′v=f(x) или

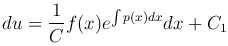
Интегрируя, получим

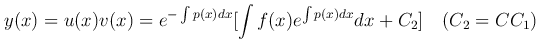
или

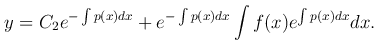
Таким образом, общее решение линейного неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения 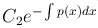и частного решения неоднородного уравнения .

Уравнение Бернулли

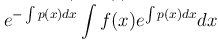Многие дифференциальные уравнения могут быть сведены к линейным путем замены переменных. Например, уравнение Бернулли, имеющее вид

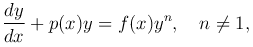
заменой переменной y^1-n=z сводится к линейному уравнению

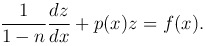
Уравнение в полных дифференциалах

Определение. Уравнением в полных дифференциалах называется уравнение

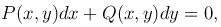
левая часть которого есть полный дифференциал некоторой функции U=U(x, y), т.е.

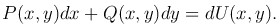
Следовательно, исходное уравнение примет вид dU(x, y)=0, тогда общий интеграл исходного уравнения определяется формулой U(x, y)=C.

Если дано начальное условие y(x_0)=y₀, то постоянная C=U(x₀, y₀) и U(x, y)=U(x₀, y₀) является частным интегралом.

Полный дифференциал выражается формулой 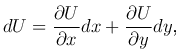, следовательно,

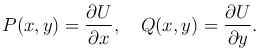
Необходимое и достаточное условие того, что выражение P(x, y)dx+Q(x, y)dy является полным дифференциалом некоторой функции, выражается равенством

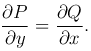
Поскольку 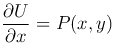, то U(x, y) = ∫ P(x, y)dx +C(y), где C(y) — произвольная функция от y. Для определения этой функции дифференцируем U(x, y) по y:

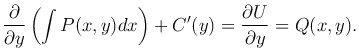
Из этого уравнения выражается C′(y) и, интегрируя, находится C(y).

Еще проще можно определить функцию U(x, y) по ее полному дифференциалу, взяв криволинейный интеграл от P(x, y)dx+Q(x, y)dy между некоторой фиксированной точкой (x₀, y₀) и точкой с переменными координатами (x, y) по любому пути:

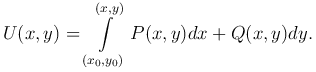
Чаще всего в качестве пути интегрирования удобно брать ломанную, составленную из двух звеньев, параллельных осям координат. В этом случае пишут

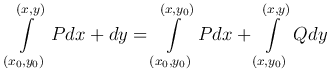
или