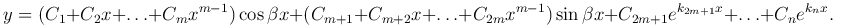Дифференциальные уравнения
Дифференциальные уравнения
 Линейные однородные уравнения n-го порядка с постоянными коэффициентами
Линейные однородные уравнения n-го порядка с постоянными коэффициентами
Определение. Линейным однородным уравнением n-го порядка с постоянными коэффициентами называется уравнение вида
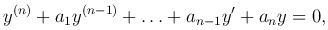
где a1, a2, …, an — действительные числа.
Решение этого уравнения будем искать в виде y=ekx (k=const). Подставляя эту функцию и ее производные
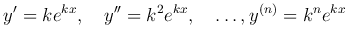
в исходное уравнение, получаем
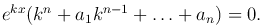
Функция y=ekx будет решением уравнения тогда и только тогда, когда
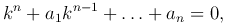
то есть, когда k — корень этого алгебраического уравнения. Это уравнение называется характеристическим уравнением. Это алгебраическое уравнение n-й степени, оно имеет n корней (считая и равные корни), среди которых могут быть и комплексные.
Рассмотрим основные возможные случаи.
1) Характеристическое уравнение имеет различные действительные корни.
Обозначим эти корни через k1, k2, …, kn (ki≠kj при i≠j). Им соответствуют решения уравнения
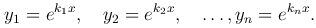
Эти функции, когда ki≠kj при i≠j, линейно-независимы на любом отрезке [a, b]. В соответствии с теоремой о структуре общего решения линейного однородного уравнения n-го порядка получаем следующее общее решение уравнения y(n)+a1y(n-1)+ … + an-1y′+any=0:
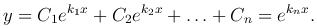
2) Характеристическое уравнение имеет действительные корни, среди которых m равны между собой.
Будем говорить в этом случае, что среди корней характеристического уравнения имеется один m-кратный корень. Обозначим его через k1. Предположим, что все остальные действительные корни различны. Корням характеристического уравнения k1=k2= … =km, km+1, …, kn соответствуют решения дифференциального уравнения
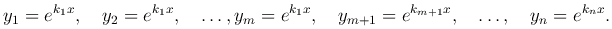
Эти решения линейно-зависимы, так как линейно-зависимы первые n функций (они равны между собой). Поэтому они не дадут общего решения дифференциального уравнения. Его надо искать в другом виде.
Сделаем замену переменных y=ek1xz. Рассмотрим
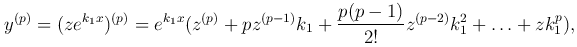
то есть производная y(p) является линейной однородной функцией z, z′, …, z(p). После подстановки в дифференциальное уравнение
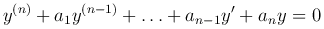
и сокращения на ek1x получим линейное однородное уравнение n-го порядка с постоянными коэффициентами:
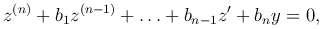
причем корни характеристического уравнения для исходного уравнения
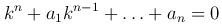
отличаются от корней характеристического уравнения для преобразованного уравнения
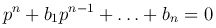
на слагаемое k1, так как между решениями y=ekx исходного уравнения и z=epx преобразованного уравнения должна быть зависимость y = z ek1x или ekx = epx ek1x, отсюда k = p + k1. Следовательно, корню k = k1 исходного уравнения соответствует корень p1 = 0 преобразованного уравнения. Кратность корня при этом сохранится.
Итак, характеристическое уравнение имеет корень p1 = 0 кратности m. Следовательно, левая часть его имеет общий множитель pm, то есть bn=bn-1=…=bn-m+1=0, и характеристическое уравнение имеет вид

Соответствующее линейное однородное дифференциальное уравнение

имеет частные решения 1, x, x², …, xm-1, так как уравнение не содержит производных порядка ниже, чем m.
Итак, корню p1 = 0 кратности m соответствуют частные решения z=1, z = x, z = x², …, z = xm-l. Следовательно, поскольку y = z ek1x, корню k1 кратности m исходного уравнения будут соответствовать m частных решений
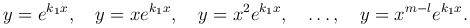
А эти решения являются линейно независимыми.
Таким образом, общее решение уравнения
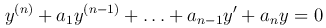
имеет вид
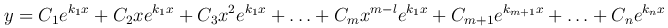
или
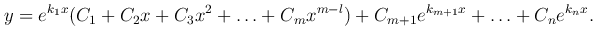
3) Характеристическое уравнение имеет простые комплексно-сопряженные корни.
Обозначим эти корни k1 = α - iβ, k2 = a + iβ, где α, β — действительные числа, 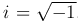 . Им соответствуют комплексные решения дифференциального уравнения (формула Эйлера)
. Им соответствуют комплексные решения дифференциального уравнения (формула Эйлера)
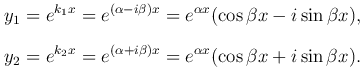
На основании третьей теоремы о свойствах решений линейного однородного уравнения наше уравнение будет иметь также и действительные решения

Если все остальные корни k3, k4, …, kn являются действительными и различными, то общее решение уравнения
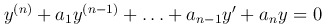
определяется формулой
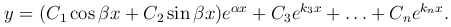
В частном случае, когда характеристическое уравнение имеет чисто мнимые корни k1 = -iβ, k2 = iβ (α = 0), получим общее решение
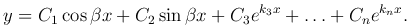
4) Характеристическое уравнение имеет кратные комплексные корни.
Пусть комплексно-сопряженные корни k1 = α - iβ, k2 = a + iβ являются m-кратными. Им соответствуют решения
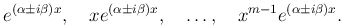
Применяя формулу Эйлера и отделяя действительную и мнимую части, получим 2m линейно-независимых решения:
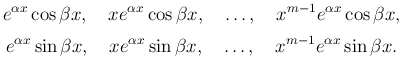
Если остальные n-2m корней km+1, …, kn являются действительными и различными, то общее решение дифференциального уравнения имеет вид
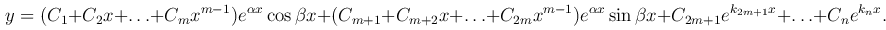
В частном случае, когда характеристическое уравнение имеет чисто мнимые корни k1 = -iβ, k2 = iβ (α = 0), получим общее решение