Линейные дифференциальные уравнения n-го порядка

Определение. Линейным дифференциальным уравнением n-го порядка называется уравнение вида

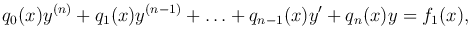
где y=y(x) — искомая функция; f₁(x), q_k(x) (k=0, …, n) — заданные функции.

Будем считать, что эти функции определены и непрерывны на некотором отрезке [a, b].

Если f₁≡0, то данное уравнение называется линейным однородным, если f₁≠0 — линейным неоднородным.

При q₀(x)≠0 линейное неоднородное уравнение после деления на q₀(x) можно привести к виду

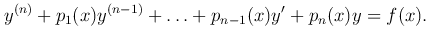
Линейное однородное уравнение при q₀(x)≠0 приводится к виду

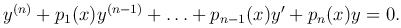
Последнее уравнение кратко запишем так:

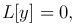
где

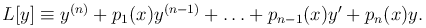
Будем называть L линейным дифференциальным оператором.

Свойства линейного дифференциального оператора:

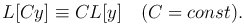
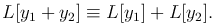
1) Постоянный множитель выносится за знак линейного оператора:
2) Линейный дифференциальный оператор, примененный к сумме двух функций y₁ и y₂, равен сумме результатов применения того же оператора к каждой функции в отдельности:

Следствие. 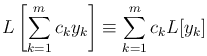, где c_k — постоянные.

Свойства решений линейного однородного уравнения n-го порядка

Теорема. Если y₁ — решение линейного однородного уравнения L[y₁]=0, то Cy₁, где C — постоянная, также является решением этого уравнения.

Теорема. Если y₁ и y₂ — два решения линейного однородного уравнения L[y]=0, то их сумма y₁+y₂ также является решением этого уравнения.

Следствие. Если y₁, y₂, …, у_n — решения уравнения L[y]=0, то функция

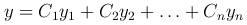
также является решением этого уравнения.

Теорема. Если уравнение L[y]=0 с действительными коэффициентами p_k(x) (k=1, 2, …, n) имеет комплексное решение y(x) =u(x) + iv(x), то действительная u(x) и мнимая v(x) части также являются решениями этого уравнения.

Замечание. Свойства оператора L здесь применены к комплексной функции действительной переменной. Это допустимо, поскольку при выводе этих формул использовались свойства производных (Cy)′=Cy′, (y₁+y₂)′=у₁′+у₂′, остающиеся справедливыми и для комплексных функций действительной переменной. Производная комплексной функции действительной переменной определяется формулой