Асимптоты графика функции

Определение. Говорят, что прямая x=a является вертикальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений

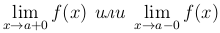
равно +∞ или -∞.

Пример. График функции y=1/x имеет вертикальную асимптоту x=0.

Определение. Говорят, что прямая Y=kx+b является наклонной асимптотой графика функции y=f(x) при x→+∞, если функция f(x) представима в виде \begin{displaymath} f(x) = kx+b+α(x), \end{displaymath}

где .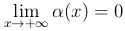

Теорема. Для того, чтобы график функции y=f(x) имел при x→+∞ наклонную асимптоту Y=kx+b, необходимо и достаточно, чтобы существовали два предельных значения

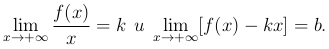
Замечание. Аналогично определяется наклонная асимптота для случая x→-∞.

Пример. График функции y=(2x²+x)/(x+1)=2x-1+1/(x+1) имеет наклонную асимптоту Y=2x-1 и при x→+∞ и при x→-∞, и, кроме того, имеет вертикальную асимптоту x=-1.

Схема исследования графика функции

1. Найти область определения функции, ее точки разрыва.
2. Изучить изменение функции при стремлении аргумента к концам промежутков области определения.
3. Найти точки экстремумов, промежутки возрастания и убывания функции.
4. Вычислить значения экстремумов, построить соответствующие точки.
5. Определить промежутки выпуклости вниз и вверх графика, найти точки перегиба.
6. Найти точки пересечения графика с координатными осями.
7. Найти асимптоты графика функции.

Вектор-функция скалярного аргумента

Определение. Переменная векторная величина u называется вектор-функцией (или векторной функцией) скалярного аргумента t, если каждому значению t₀∈ T, T — некоторый интервал, соответствует определенный вектор u(t₀); в этом случае пишут

u = u(t).

Если u = u(t), то и проекции u_x, u_y, u_z переменного вектора u на оси декартовой системы координат будут скалярными функциями аргумента t:

u_x=u_x(t), u_y=u_y(t), u_z=u_z(t).

Пример вектор функции скалярного аргумента. Рассмотрим точку M(x, y, z), движущуюся по некоторой линии γ в пространстве. Радиус-вектор 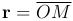точки M будет иметь определенное направление и длину в фиксированный момент времени t.

Таким образом, имеем дело с переменным вектором 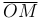или переменной векторной величиной

r = r(t),

зависящей от времени t. Это равенство называется векторным уравнением движения точки M.

Координаты переменного вектора 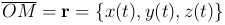являются также переменными величинами (скалярными), зависящими от времени t:

x=x(t), y=y(t), z=z(t).

Эти уравнения называются параметрическими уравнениями рассматриваемой линии γ.

Предел и непрерывность вектор-функции

Определение. Вектор a называется пределом вектор-функции r=r(t) при t→ t₀, если для любого ε>0 существует такое δ=δ(ε)>0, что |r(t)-a|<ε для всех t, удовлетворяющий неравенству |t-t₀|<δ, t ≠ t₀.

Обозначения предела вектор-функции:

r(t) → a при t → t₀.

Утверждение. Если r(t)=(x(t), y(t), z(t)) и a=(a₁, a₂, a₃), то 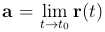эквивалентно

Свойства предела вектор-функции

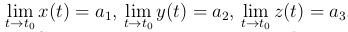
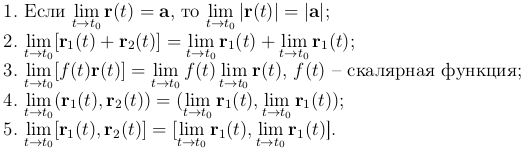
Определение. Вектор-функция r=r(t), определенная в некоторой окрестности t=t₀, называется непрерывной в точке t=t₀, если

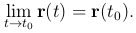
Утверждение. Вектор-функция r(t)=(x(t), y(t), z(t)) непрерывна в точке t₀ тогда и только тогда, когда функции x(t), y(t), z(t).

Производная вектор-функции

Определение. Пусть вектор-функция r=r(t) определена в окрестности точки t=t₀. Если существует предел 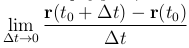, то он называется производной вектор-функции r=r(t) в точке t₀.

Обозначения: .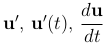

Утверждение. r имеет в точке t₀ производную тогда и только тогда, когда x(t), y(t), z(t) имеют производные в точке t₀ и 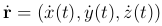.