Понятие непрерывности функции

Пусть точка a принадлежит области задания функции f(x) и любая ε-окрестность точки a содержит отличные от a точки области задания функции f(x), т.е. точка a является предельной точкой множества {x}, на котором задана функция f(x).

Определение. Функция f(x) называется непрерывной в точке a, если функция f(x) имеет в точке a предел и этот предел равен частному значению f(a) функции f(x) в точке a.

Из этого определения имеем следующее условие непрерывности функции f(x) в точке a:

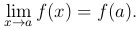
Так как 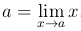, то мы можем записать

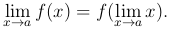
Следовательно, для непрерывной в точке a функции символ 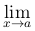предельного перехода и символ f характеристики функции можно менять местами.

Определение. Функция f(x) называется непрерывной справа (слева) в точке a, если правый (левый) предел этой функции в точке a существует и равен частному значению f(a) функции f(x) в точке a.

Тот факт, что функция f(x) непрерывна в точке a справа записывают так:

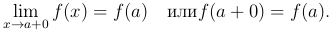
А непрерывность функции f(x) в точке a слева записывают как:

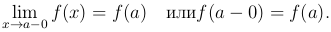
Замечание. Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва этой функции.

Теорема. Пусть на одном и том же множестве заданы функции f(x) и g(x), непрерывные в точке a. Тогда функции f(x)+g(x), f(x)-g(x), f(x) · g(x) и f(x)/g(x) — непрерывны в точке a (в случае частного нужно дополнительно требовать g(a) ≠ 0).

Непрерывность основных элементарных функций

1) Степенная функция y=xⁿ при натуральном n непрерывна на всей числовой прямой.

Сначала рассмотрим функцию f(x)=x. По первому определению предела функции в точке a возьмем любую последовательность {x_n}, сходящуюся к a, тогда соответствующая последовательность значений функций {f(x_n)=x_n} также будет сходиться к a, то есть 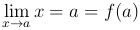, то есть функция f(x)=x непрерывная в любой точек числовой прямой.

Теперь рассмотрим функцию f(x)=xⁿ, где n — натуральное число, тогда f(x)=x · x · … · x. Перейдем к пределу при x → a, получим 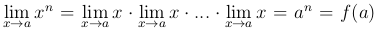, то есть функция f(x)=xⁿ непрерывна на числовой прямой.

2) Показательная функция.

Показательная функция y=a^x при a>1 является непрерывной функцией в любой точке бесконечной прямой.

Показательная функция y=a^x при a>1 удовлетворяет условиям: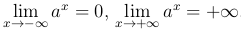

3) Логарифмическая функция.

Логарифмическая функция непрерывна и возрастает на всей полупрямой x>0 при a>1 и непрерывна и убывает на всей полупрямой x>0 при 0<a<1, причем

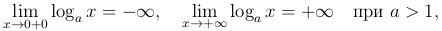
4) Гиперболические функции.

Гиперболическими функциями называются следующие функции:

1. Гиперболический синус
2. Гиперболический косинус
3. Гиперболический тангенс
4. Гиперболический котангенс

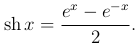
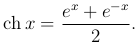
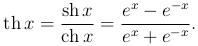
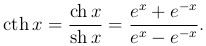
Из определения гиперболических функции следует, что гиперболический косинус, гиперболический синус и гиперболический тангенс заданы на всей числовой оси, а гиперболический котангенс определен всюду на числовой оси, за исключением точки x=0.

Гиперболические функции непрерывны в каждой точке области их задания (это следует из непрерывности показательной функции и теоремы об арифметических действиях).

5) Степенная функция

Степенная функция y=x^α=a^{α log_ax} непрерывна в каждой точке открытой полупрямой x>0.

6) Тригонометрические функции.

Функции sin x и cos x непрерывны в каждой точке x бесконечной прямой. Функция y=tg x непрерывна на каждом из интервалов (kπ-π/2,kπ+π/2), а функция y=ctg x непрерывна на каждом из интервалов ((k-1)π,kπ) (здесь всюду k — любое целое число, т.е. k=0, ±1, ±2, …).

7) Обратные тригонометрические функции.

Функции y=arcsin x и y=arccos x непрерывны на отрезке [-1, 1]. Функции y=arctg x и y=arcctg x непрерывны на бесконечной прямой.

Два замечательных предела

Теорема. Предел функции (sin x)/x в точке x=0 существует и равен единице, т.е.

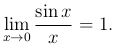
Этот предел называется первым замечательным пределом.

Доказательство. При 0<x<π/2 справедливы неравенства 0<\sin x<x<tg x. Разделим эти неравенства на sin x, тогда получим

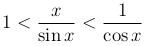
или

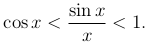
Эти неравенства справедливы также и для значений x, удовлетворяющих условиям -π/2<x<0. Это следует из того, что cos x=cos(-x) и 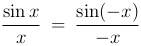. Так как cos x — непрерывная функция, то 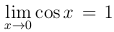. Таким образом, для функций cos x, 1 и 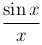в некоторой δ-окрестности точки x=0 выполняются все условия теорем. Следовательно, .

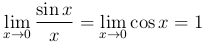Теорема. Предел функции 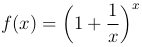при x → ∞ существует и равен числу e:

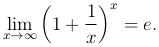
Этот предел называется вторым замечательным пределом.

Замечание. Верно также, что

Непрерывность сложной функции

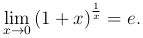
Теорема. Пусть функция x=φ(t) непрерывна в точке a, а функция y=f(x) непрерывна в точке b=φ(a). Тогда сложная функция y=f[φ(t)]=F(t) непрерывна в точке a.

Пусть x=φ(t) и y=f(x) — простейшие элементарные функции, причем множество значений {x} функции x=φ(t) является областью задания функции y=f(x). Как мы знаем, элементарные функции непрерывны в каждой точке области задания. Поэтому по предыдущей теореме сложная функция y=f(φ(t)), то есть суперпозиция двух элементарных функций, непрерывна. Например, функция 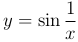непрерывна в любой точке x ≠ 0, как сложная функция от двух элементарных функций x=t^-1 и y=sin x. Также функция y=ln sin x непрерывна в любой точке интервалов (2kπ,(2k+1)π), k ∈ Z (sin x>0).