Производная функции

{\large\bf Производная функции}

Рассмотрим функцию y=f(x), заданную на интервале (a, b). Пусть x — любое фиксированная точка интервала (a, b), а Δx — произвольное число, такое, что значение x+Δx также принадлежит интервалу (a, b). Это число Δx называют приращением аргумента.

Определение. Приращением функции y=f(x) в точке x, соответствующим приращению аргумента Δx, назовем число

Δy = f(x+Δx) - f(x).

Считаем, что Δx ≠ 0. Рассмотрим в данной фиксированной точке x отношение приращения функции в этой точке к соответствующему приращению аргумента Δx

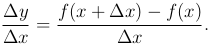
Это отношение будем называть разностным отношением. Так как значение x мы считаем фиксированным, разностное отношение представляет собой функцию аргумента Δx. Эта функция определена для всех значений аргумента Δx, принадлежащих некоторой достаточно малой окрестности точки Δx=0, за исключением самой точки Δx=0. Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0.

Определение. Производной функции y=f(x) в данной фиксированной точке x называется предел при Δx → 0 разностного отношения, то есть

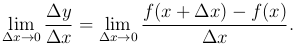
При условии, что этот предел существует.

Обозначение. y′(x) или f′(x).

Геометрический смысл производной: Производная от функции f(x) в данной точке x равна тангенсу угла между осью Ox и касательной к графику этой функции в соответствующей точке:

f′(x₀) = \tgα.

Механический смысл производной: Производная от пути по времени равна скорости прямолинейного движения точки:

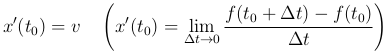
Уравнение касательной к линии y=f(x) в точке M₀(x₀,y₀) принимает вид

y-y₀ = f′(x₀) (x-x₀).

Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f′(x₀)≠ 0, то уравнение нормали к линии y=f(x) в точке M₀(x₀,y₀) записывается так:

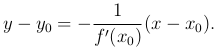
Понятие дифференцируемости функции

Пусть функция y=f(x) определена на некотором интервале (a, b), x — некоторое фиксированное значение аргумента из этого интервала, Δx — любое приращение аргумента, такое, что значение аргумента x+Δx ∈ (a, b).

Определение. Функция y=f(x) называется дифференцируемой в данной точке x, если приращение Δy этой функции в точке x, соответствующее приращению аргумента Δx, может быть представимо в виде

Δy = A Δx +αΔx,

где A — некоторое число, не зависящее от Δx, а α — функция аргумента Δx, являющая бесконечно малой при Δx→ 0.

Так как произведение двух бесконечно малых функций αΔx является бесконечно малой более высокого порядка, чем Δx (свойство 3 бесконечно малых функций), то можем записать:

Δy = A Δx +o(Δx).

Теорема. Для того, чтобы функция y=f(x) являлась дифференцируемой в данной точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную. При этом A=f′(x), то есть

Δy = f′(x) Δx +o(Δx).

Операцию нахождения производной обычно называют дифференцированием.

Теорема. Если функция y=f(x) дифференцируема в данной точке x, то она непрерывна в этой точке.

Замечание. Из непрерывности функции y=f(x) в данной точке x, вообще говоря, не вытекает дифференцируемость функции f(x) в этой точке. Например, функция y=|x| — непрерывна в точке x=0, но не имеет производной.

Понятие дифференциала функции

Определение. Дифференциалом функции y=f(x) называется произведение производной этой функции на приращение независимой переменной x:

dy = y′ Δx, df(x) = f′(x) Δx.

Для функции y=x получаем dy=dx=x′Δx = 1· Δx= Δx, то есть dx=Δx — дифференциал независимой переменной равен приращению этой переменной.

Таким образом, можем записать

dy = y′ dx, df(x) = f′(x) dx

или

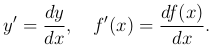
Дифференциал dy и приращение Δy функции y=f(x) в данной точке x, оба отвечающие одному и тому же приращению аргумента Δx, вообще говоря, не равны друг другу.

Геометрический смысл дифференциала: Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение Δx.

Правила дифференцирования

Теорема. Если каждая из функций u(x) и v(x) дифференцируема в данной точке x, то сумма, разность, произведение и частное этих функций (частное при условии, что v(x)≠ 0) также дифференцируемы в этой точке, причем имеют место формулы:

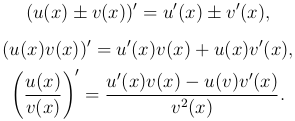
Рассмотрим сложную функцию y=f(φ(x))≡ F(x), где y=f(u), u=φ(x). В этом случае u называют промежуточным аргументом, x — независимой переменной.

Теорема. Если y=f(u) и u=φ(x) — дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна произведению этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.

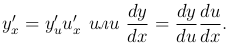
Замечание. Для сложной функции, являющейся суперпозицией трех функций y=F(f(φ(x))), правило дифференцирования имеет вид

y′_x = y′_u u′_v v′_x,

где функции v=φ(x), u=f(v) и y=F(u) — дифференцируемые функции своих аргументов.

Теорема. Пусть функция y=f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x₀. Пусть, кроме того, эта функция дифференцируема в указанной точке x₀ и ее производная в этой точке f′(x₀) ≠ 0. Тогда в некоторой окрестности соответствующей точки y₀=f(x₀) определена обратная для y=f(x) функция x=f^-1(y), причем указанная обратная функция дифференцируема в соответствующей точке y₀=f(x₀) и для ее производной в этой точке y справедлива формула

Таблица производных

Инвариантность формы первого дифференциала

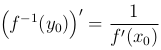
Рассмотрим дифференциал сложной функции. Если y=f(x), x=φ(t) — дифференцируемы функции своих аргументов, то производная функции y=f(φ(t)) выражается формулой

y′_t = y′_x x′_t.

По определению dy=y′_tdt, тогда получим

dy = y′_tdt = y′_x · x′_tdt = y′_x(x′_tdt) = y′_xdx,

то есть

dy = y′_xdx.

Итак, доказали,

Свойство инвариантности формы первого дифференциала функции: как в случае, когда аргумент x является независимой переменной, так и в случае, когда аргумент x сам является дифференцируемой функцией новой переменной, дифференциал dy функции y=f(x) равен производной этой функции, умноженной на дифференциал аргумента dx.

Применение дифференциала в приближенных вычислениях

Мы показали, что дифференциал dy функции y=f(x), вообще говоря, не равен приращению Δy этой функции. Тем не менее с точностью до бесконечно малой функции более высокого порядка малости, чем Δx, справедливо приближенное равенство

Δy ≈ dy.

Отношение 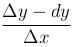называют относительной погрешностью равенства этого равенства. Так как Δy-dy=o(Δx), то относительная погрешность данного равенства становится как угодно малой при уменьшении |Δх|.

Учитывая, что Δy=f(x+δ x)-f(x), dy=f′(x)Δx, получим f(x+δ x)-f(x) ≈ f′(x)Δx или

f(x+δ x) ≈ f(x) + f′(x)Δx.

Это приближенное равенство позволяет с ошибкой o(Δx) заменить функцию f(x) в малой окрестности точки x (т.е. для малых значений Δx) линейной функцией аргумента Δx, стоящей в правой части.

Производные высших порядков

Определение. Второй производной (или производной второго порядка) функции y=f(x) называется производная от ее первой производной.

Обозначение второй производной функции y=f(x):

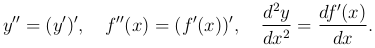
Механический смысл второй производной. Если функция y=f(x) описывает закон движения материальной точки по прямой линии, то вторая производная f″(x) равна ускорению движущейся точки в момент времени x.

Аналогично определяется третья, четвертая производная.

Определение. n-й производной (или производной n-го порядка) функции y=f(x) называется производная от ее n-1-й производной:

y⁽ⁿ⁾=(y^(n-1))′, f⁽ⁿ⁾(x)=(f^(n-1)(x))′.

Обозначения: y″′, y^IV, y^V и т.д.