Элементы дифференциальной геометрии поверхностей и кривых

Определение. Годографом векторной функции r(t) называется геометрическое место концов всех векторов r(t), приложенных к началу координат O.

Геометрический смысл производной: Производная вектор—функции в данной точке есть вектор, направленный по касательной к годографу данной вектор—функции в соответствующей точке.

Физический смысл производной: Так как векторная функция r=r(t) определяет закон движения материальной точки по кривой L, представляющей собой годограф этой функции, то производная r′(t) равна скорости движения по указанной прямой.

Уравнение касательной к кривой L в точке r(t₀), для которой r′(t₀)≠ 0, в векторной записи имеет вид

r = r(t₀) + r′(t₀)τ, τ∈(-∞,+∞),

где r — текущий радиус—вектор касательной.

В координатной записи уравнение касательной имеет вид

x=x(t₀)+x′(t₀)τ, y=y(t₀)+y′(t₀)τ,
z=z(t₀)+z′(t₀)τ, τ∈(-∞,+∞).

Исключив переменную τ, получим

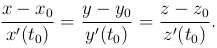
Уравнение нормальной плоскости к пространственной кривой

x=x(t), y=y(t), z=z(t)

в точке M₀(x₀,y₀z₀), которой соответствует значение параметра t₀, имеет вид

x′(t₀)(x-x₀)+y′(t₀)(y-y₀)+z′(t₀)(z-z₀)=0.

Интерполяция и численное дифференцирование

Простейшая задача интерполирования. Интерполяционная формула Лагранжа

Пусть для некоторой функции f(x) вычислены ее значения в точках x₁, x₂,…, x_n. Требуется восстановить ее значения при других x.

Обычно задачу понимают следующим образом. Ищется целый многочлен L(x) наинизшей степени, который в заданных точках x_i (i=1, 2, …, n), называемых узлами интерполирования, принимает те же значения f(x_i), что и функция f(x), то есть L(x_i)=f(x_i), и приближенно полагают для любых x:

f(x) = L(x).

Это приближенное равенство называется интерполяционной формулой.

Для разыскания многочлена L(x), удовлетворяющего условиям

L(x_i) = f(x_i), (i=1, 2, …, ),

удобно ввести многочлен (n-1)-й степени

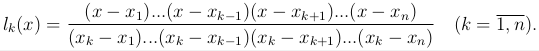
Видно, что

l_k(x_k) = 1, l_k(x_i)=0, k ≠ i.

Тогда многочлен

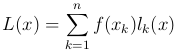
удовлетворяет условиям L(x_i)=f(x_i) (i=1, 2, …, n). Этот многочлен называется интерполяционным многочленом Лагранжа.

В этом случае приближенное равенство

f(x) = L(x)

называется интерполяционной формулой Лагранжа.

Многочлен l_k(x) можем записать более сжато, если ввести выражение

ω(x) = (x-x₁)…(x-x_n),

очевидно, что ω(x_k)=0 (k=1, 2, …, n). Следовательно,

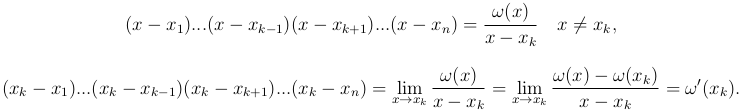
Таким образом,

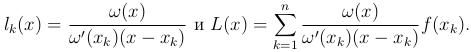
Теперь оценим разность между f(x) и L(x). Предположим, что f⁽ⁿ⁾(x) — непрерывна. Положим

φ(t) = f(t) - L(x) - Kω(t),

где K выбирается из условия φ(x) = 0 (x — точка, в которой оценивается погрешность).

Из уравнения φ(x)=0 получим

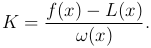
При таком выборе K функция φ(t) обращается в нуль в (n+1)-й точке: x₁, x₂, …, x_n, x. На основании теоремы Ролля ее производная φ′(t) обращается в нуль по-крайней мере в n точках. Применяя теорему Ролля к φ′(t), получим, что φ″(t) обращается в нуль в (n-1)-1 точке и т.д. φ⁽ⁿ⁾(t) обращается в нуль по крайней мере в одной точке ξ∈[y₁,y₂], где

y₁ = min {x₁, x₂, …, x_k, x}, y₂ = max {x₁, x₂, …, x_k, x}.

Так как φ⁽ⁿ⁾(t)=f⁽ⁿ⁾(t)-Kn!, то из условия φ⁽ⁿ⁾}(ξ)=0 получим

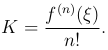
Следовательно, уравнение φ(x) = 0 можем записать в виде

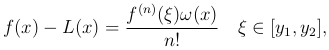
которое дает представление остаточного члена.

Интерполяционная формула Ньютона с разделенными разностями

Введем понятие разделенной разности. Разделенные разности нулевого порядка f(x_i) совпадают со значениями функции f(x_i); разности первого порядка определяются равенством

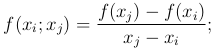
разности второго порядка — равенством

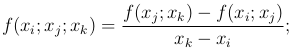
разности k-го порядка определяются через разности (k-1)-го порядка

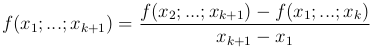
Утверждение. Справедливо равенство

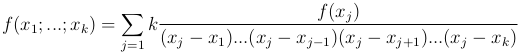
При помощи разделенных разностей можно получить другую форму интерполяционного многочлена L(x).

Справедливо равенство

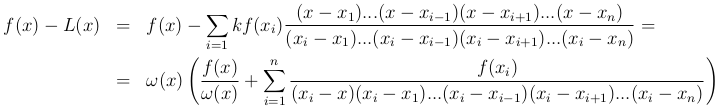
Сравнивая с равенством в утверждении, получим

f(x)-L(x) = f(x; x₁; …; x_n)ω(x).

Интерполяционный многочлен Лагранжа можно представить в виде:

L(x) = L₁(x)+(L₂(x)-L₁(x))+…+(L_n(x)-L_n-1(x)),

где L_i(x) — интерполяционный многочлен Лагранжа с узлами интерполяции x₁, …, x_i (i=1, 2, …, n).

Так как L_m-1(x_j)=L_m(x_j)=f(x_j) для j=1, 2, …, m-1, то разность L_m(x)-L_m-1(x) есть многочлен степени m-1, обращающийся в нуль в точках x₁, …, x_m-1. Следовательно,

L_m(x) - L_m-1(x) = A_m-1ω_m-1(x),

где A_m-1=const. Полагая x=x_m, получим

f(x_m) - L_m-1(x_m) = A_m-1ω_m-1(x_m).

С другой стороны, полагая в новом представлении интерполяционной формулы Лагранжа n=m-1 и x=x_m, получим

f(x_m) - L_m-1(x_m) = f(x_m; x₁; …; x_m-1)ω_m-1(x_m).

Таким образом, A_m-1 = f(x₁; …; x_m) и поэтому

L_m(x) - L_m-1(x) = f(x₁;…;x_m)ω_m-1(x).

Окончательно получим \begin{displaymath} L_n(x) = f(x₁) + f(x₁; x₂)(x₁-x₂) + … + f(x₁; …; x_n)(x-x₁)…(x-x_n-1).

Интерполяционный многочлен, записанный в такой форме, называется интерполяционным многочленом Ньютона с разделенными разностями.

Численное дифференцирование

Простейшие формулы численного дифференцирования получаются в результате дифференцирования интерполяционных формул.

Пусть известны значения функции в точках x₁, …, x_n и требуется вычислить производную f^(k)(x₀). Построим интерполяционный многочлен L(x) и положим f^(k)(x₀) ≈ L^(k)(x₀).

Другой способ построения формул численного дифференцирования — это метод неопределенных коэффициентов. Коэффициенты c_i формулы численного дифференцирования

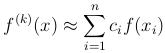
выбираются из условия, чтобы формула была точна для многочленов максимально высокой степени. Возьмем 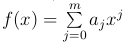и потребуем, чтобы для такого многочлена последнее соотношение обратилось в равенство

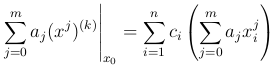
Чтобы равенство выполнялось для любого многочлена степени m, необходимо и достаточно, чтобы коэффициенты при a_j в правой и левой частях были равны. Поскольку

(x^j)^(k) = j(j-1) … (j-k+1)x^j-k,

то получаем линейную систему уравнений

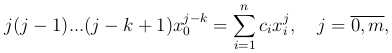
относительно неизвестных c_i. Если m=n-1, то число уравнений равно числу неизвестных, причем определитель этой системы будет отличен от нуля. Таким образом, всегда можно построить формулу численного дифференцирования с n узлами, точную для многочленов степени n-1.