Раскрытие неопределенностей (правило Лопиталя).

Раскрытие неопределенности вида 0/0

Будем говорить, что отношение двух функций f(x)/g(x) представляет собой при x → a неопределенность вида 0/0, если

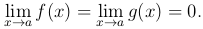
Раскрыть эту неопределенность — это значит вычислить предел 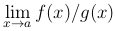(при условии, что этот предел существует).

Теорема [первое правило Лопиталя]. Пусть две функции f(x) и g(x) определены и дифференцируемы всюду в некоторой окрестности точки a, за исключением, быть может, самой точки a, и, кроме того, производная g′(x) не обращается в нуль всюду в указанной выше окрестности точки a. Пусть, далее,

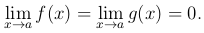
Тогда если существует (конечный или бесконечный) предел

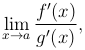
то существует и предел

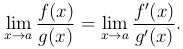
Замечание 1. Правило Лопиталя «действует» не всегда, т.е. предел отношения функций может существовать и в случае, когда предела отношения производных не существует.

Например, при a=0, 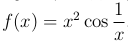, g(x)=sin x существует предел

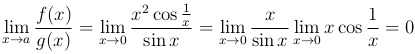
в то время как предел

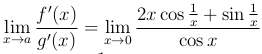
не существует (в силу того, что не существует предел 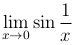, а предел 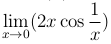существует и равен нулю).

Замечание 2. Если производные f′(x) и g′(x) удовлетворяют тем же требованиям, что и сами функции f(x) и g(x), то правило Лопиталя можно применять повторно, т.е. предел отношения первых производных функций f(x) и g(x) можно заменить пределом отношения вторых производных этих функций. Мы получим при этом, что

Раскрытие неопределенности вида ∞/∞

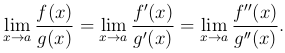
Будем говорить, что отношение двух определенных в окрестности точки a функций f(x) и g(x) представляет собой при x → a неопределенность вида ∞/∞, если

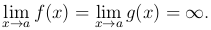
Для раскрытия этой неопределенности, т.е. для вычисления предела

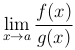, справедливо утверждение, полностью аналогичное первому правилу Лопиталя.

Теорема [второе правило Лопиталя]. Пусть две функции f(x) и g(x) определены и дифференцируемы всюду в некоторой окрестности точки a, за исключением, быть может, самой точки a, и, кроме того, производная g′(x) не обращается в нуль всюду в указанной выше окрестности точки a. Пусть, далее,

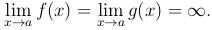
Тогда если существует (конечный или бесконечный) предел

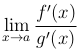
то существует и предел

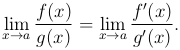
Раскрытие неопределенностей других видов

Кроме изученных выше неопределенностей видов 0/0 и ∞/∞, часто встречаются неопределенности следующих видов: 0·∞, ∞-∞, 1^∞, 0^∞, ∞⁰.

Все эти неопределенности сводятся к изученным выше двум неопределенностям путем алгебраических преобразований. Покажем это, например, по отношению к последним трем из указанных выше неопределенностей. Каждая из этих неопределенностей имеет вид

y=f(x)^g(x),

где при x → a функция f(x) стремится соответственно к 1, 0 или ∞, a g(x) стремится соответственно к ∞ или 0. Данное выражение сначала логарифмируют (считая, что f(x)>0)

ln y=g(x) ln f(x),

а потом находят предел его логарифма.

Заметим, что в любом из трех рассматриваемых случаев этот логарифм представляет собой при x → a неопределенность вида 0·∞. Значит, достаточно научиться сводить неопределенность такого вида к неопределенности вида 0/0 или ∞/∞. Покажем, как это делается. Итак, пусть

z=φ(x)ψ(x),

причем

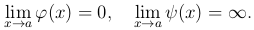
Перепишем наше выражение в виде

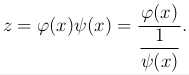
Очевидно, последнее выражение представляет собой при x → a неопределенность вида 0/0.

Аналогично раскрывается неопределенность вида ∞-∞, т.е. находится предел

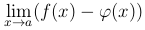
при условии, что 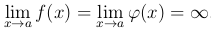. С помощью преобразования

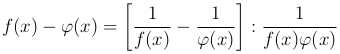
эта неопределенность сводиться к неопределенности вида 0/0. \underline{Пример.} Вычислить 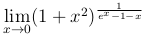. Пусть 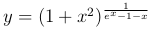. Тогда,

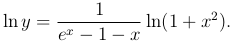
Пользуясь правилом Лопиталя, получим

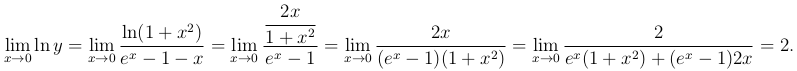
Отсюда ясно, что 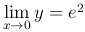.