Предельное значение функции

Понятие функции

Пусть задана переменная величина x, имеющая областью изменения некоторое множество {x}. Если каждому значению переменной x из множества {x} ставится в соответствие по известному закону некоторое число y, то говорят, что на множестве {x} задана функция y=y(x) или y=f(x). При этом переменная x называется аргументом или независимой переменной, множество {x} называется областью задания функции, а то число y, которое соответствует данному значению x, называется частным значением функции в точке x. Совокупность всех частных значений образует вполне определенное множество {y}, которое называют либо областью изменения функции, либо множеством всех значений функции.

В обозначении y=f(x) букву f часто называют характеристикой функции. Для обозначения аргумента, функции и ее характеристики могут употребляться различные символы.

Способы задания функций:

С1. Аналитический: когда посредством формул задается закон, устанавливающий соответствие между множеством всех значений аргумента и множеством всех значений функции.
C2. Табличный: задается таблица отдельных значений аргумента и соответствующие им значения функции. При таком способе задания можно приближенно вычислить не содержащиеся в таблице значения функции, отвечающие промежуточным значениям аргумента. Для этого применяется метод интерполяции, заключающийся в замене функции между ее соседними табличными значениями какой-либо функцией простой природы (например, линейной или квадратичной). Примером табличного способа задания функции может служить расписание движения поезда, которое определяет местоположение поезда в отдельные моменты времени. Интерполяция позволяет приближенно определить местоположение поезда в любой промежуточный момент времени.
C3. Графический: соответствие между аргументом и функцией задается посредством графика.

Сложная функция. Функции, полученные в результате суперпозиции двух или нескольких функций, мы будем называть сложными. Под суперпозицией двух функций мы понимаем функцию, полученную в результате наложения или последовательного применения указанных двух функций в определенном порядке.

Сложные функции определяются следующим образом. Пусть функция x=φ(t) задана на множестве {t}, и пусть {x} — множество ее значений. Допустим, что на множестве {x} задана функция y=f(x). Тогда говорят, что на множестве {t} задана сложная функция y=f[φ(t)]=F(t) или y=f(x), где х=φ(t).

К основным элементарным функциям относятся тригонометрические функции (y=cos x, y=sin x, y=tg x, y=ctg x), обратные тригонометрические функции (y=arccos x, y=arcsin x, y=arctg x, y=arcctg x), степенная функция y=x^a, показательная y=a^x, логарифмическая y=log_a x.

Элементарными функциями называются функции, которые можно получить из основных элементарных функций с помощью алгебраических действий и образования сложных функций. Например, функции y=lg cos 2x, y=x²+tg x, y=5^{arctg x+ lg x} и т.п.

Определение предельного значения функции

Пусть функция y=f(x) определена на некотором множестве {x}, и пусть a — точка, предельная для этого множества.

Определение. Число b называется предельным значением функции y=f(x) в точке x=a (или пределом функции при x → a), если для любой последовательности значений аргумента x₁, x₂, …, x_n, …, сходящейся к a и состоящей из чисел x_n, отличных от a, соответствующая последовательность значений функции f(x₁), f(x₂), …, f(x_n), … сходится к b.

Другое определение предела функции.

Определение. Число b называется пределом функции y=f(x) при x \to a, если для любого числа ε>0 существует такое δ>0, что при всех x, удовлетворяющих условию

0 < |x-a| < δ,

выполняется неравенство

|f(x)-b|<ε.

Для обозначения предельного значения функции y=f(x) в точке a используют следующую символику:

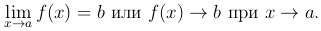
Геометрический смысл определения предела функции: Первое неравенство означает, что x ∈ O(a,δ) на оси Ox. Второе неравенство означает, что значение функции y=f(x) ∈ O(b,ε) оси Oy. Следовательно, точки M графика функции y=f(x) должны находиться в полосе шириной 2ε, ограниченной прямыми y = b ± ε для всех значений x, удаленных от точки a не далее, чем на δ.

Определение. Предел слева 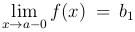, где x стремится к a, оставаясь меньше a: x<a и предел справа 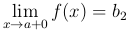, где x стремится к a, оставаясь больше a: x>a.

Утверждение. Если функция f(x) имеет в точке a как правый, так и левый пределы и если эти односторонние пределы равны одному и тому же числу b, то эта функция имеет в точке a предел, равный b. Обратно, если функция f(x) имеет в точке a равный b предел, то как правый, так и левый пределы f(x) в точке a существуют и оба равны b.

Определение. Число b называется пределом функции y=f(x) при x → ∞, если для любого положительного числа ε существует положительное число N такое, что для всех значений аргумента x, удовлетворяющих условию |x|>N, справедливо неравенство |f(x)-A|<ε.

Обозначается этот предел следующим образом:

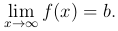
Определение. Число b называется пределом функции y=f(x) при x→+∞ (x→-∞), если для любого положительного числа ε существует положительное число N такое, что для всех значений аргумента x, удовлетворяющих условию x>N (x<-N), справедливо неравенство |f(x)-A|<ε.

Символические обозначения:

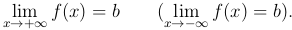
Утверждение. Функция, имеющая конечный предел в точке a локально ограничена, то есть существует окрестность точки a, на пересечении которой с множеством задания функции эта функция ограничена.

Теорема [Основная теорема]. Пусть две функции f(x) и g(x) заданы на одном и том же множестве {x} и имеют в точке a пределы, тогда сумма, разность и произведение этих функций также имеют пределы, причем

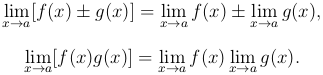
Если, кроме того, 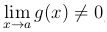, то и частное f(x):g(x) имеет предел, причем

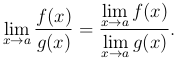
Теорема. Пусть три функции u=u(x), y=y(x), v=v(x) определены в некотором промежутке, содержащем точку a.

Если для любого x из этого промежутка выполняются неравенства

u(x) ≤ y(x) ≤ v(x)

и функции u=u(x), v=v(x) имеют одинаковые пределы при x → a, то функция y=y(x) имеет тот же предел при x → a.

Теорема. Если функции u=u(x), v=v(x) определены в некоторой δ-окрестности точки a, для всех x∈ O(a, δ), x ≠ a, выполняется неравенство u(x) < v(x) и функция и функции имеют пределы при x → a, то 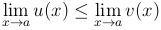.