Функции многих переменных

Rⁿ как пример метрического пространства

Определение. Произвольное множество {M}, элементы которого именуются точками, называется метрическим пространством, если существует правило, с помощью которого между двумя точками M′ и M″∈ {M} ставится в соответствие число ρ(M′,M″), называемое расстояниями между M′ и M″. При этом выполняются следующие аксиомы:

1. ρ(M′,M″)=ρ(M″,M′) (симметрия расстояния);
2. Для любых M′, M″ ρ(M′,M″) ≥ 0 и =0, если M′ совпадает с M″;
3. Для любых M′, M″, M″′, ρ(M′,M″′) ≤ ρ(M′,M″) + ρ(M″,M″′).

Отметим, что на плоскости расстояние между точками x и y:

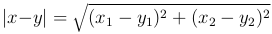
Аналогично в пространстве:

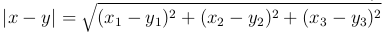
и т.д.

Определение. Точкой x n-мерного пространства называется упорядоченная совокупность n действительных чисел (x₁, …, x_n)=x. Совокупность точек n-мерного пространства, для которых определено расстояние между точками по формуле

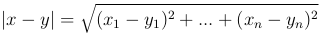
называется n-мерным евклидовым пространством и обозначается Rⁿ.

Свойства

1. |x-y|≥ 0 и |x-y|=0 равносильно x=y;
2. |x-y|=|y-x|
3. |x-z| ≤ |x-y| + |y-z|, для любых x, y, z ∈ Rⁿ.

Таким образом, Rⁿ есть метрическое пространство в смысле первого определения.

Сходимость в пространстве Rⁿ

Рассмотрим последовательность точек x¹, x², …, x^k, …, где xⁱ = (x₁ⁱ,…,x_nⁱ)∈ Rⁿ.

Определение. Последовательность {x^k} сходится к точке x⁰ из пространства Rⁿ, если |x^k-x⁰|→ 0 при k→∞, то есть если

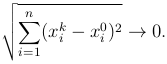
В этом случае пишут .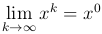

Утверждение 1. {x^k}→ x⁰ тогда и только тогда, когда {x_i^k}→ x_i⁰ для любого i.

Утверждение 2. Справедливы соотношения:

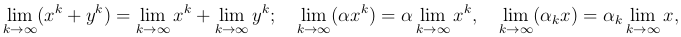
где пределы справа существуют, x^k, y^k∈ Rⁿ, α, α_k∈ R.

Определение. Множество точек x(t)∈ Rⁿ, t∈(a,b)∈ R, называется непрерывной кривой в Rⁿ, если |x(t)-x(t₀)|→ 0 при t→ t₀, t, t₀∈(a,b).

Утверждение. x(t)→ x(t₀) тогда и только тогда, когда x_j(t)→ x_j(t₀) (j=1, 2, …, n).

Открытые множества в Rⁿ. Топология в Rⁿ

Определение. Пусть x⁰∈ Rⁿ и ε>0. Множество точек x∈ Rⁿ таких, что |x-x⁰|<ε, называется n-мерным шаром с центром в точке x⁰ и радиуса ε. Если здесь |x-x⁰|≤ε, то шар называется замкнутым.

Определение. Пусть Ω — произвольное множество в Rⁿ. Точка x⁰∈ Rⁿ называется внутренней точкой Ω, если существует открытый шар с центром в x₀, полностью лежащий в Ω.

Определение. Множество Ω называется открытым, если все его точки являются внутренними.

Примеры открытых множеств:

1. (a, b)∈ R;
2. Открытый шар |x-x⁰|<r.

Теорема. Пересечение конечного числа, так же как и объединение любой совокупности открытых множеств, является открытым множеством.

Теорема. Множество E называется топологическим пространством, если в нем выделено семейство частей, называемых открытыми в этой топологии, удовлетворяющие свойствам:

1. E и ∅ — открытые;
2. пересечение конечного числа открытых множеств — открыто;
3. объединение конечного или бесконечного числа открытых множеств

— открыто.

В силу этого определения и теоремы получаем, что Rⁿ является топологическим пространством.

Определение. Всякое открытое множество Ω ⊂ Rⁿ, содержащее точку x⁰, называется окрестностью этой точки.

Определение. Множество Ω называется связным, если любые точки x′, x″∈ Ω можно соединить непрерывной кривой x(t) ⊂ Ω, где 0≤ t≤ 1: x(0)=x′, x(1)=x″.

Определение. Связное открытое множество называется областью.

Определение. Точка x⁰∈Ω называется граничной, если в любой окрестности этой точки есть точки, как принадлежащие, так и не принадлежащие Ω. Границей множества называется совокупность всех его граничных точек. Если к области присоединить границу, то полученное множество называется замкнутым. Ограниченным множеством называется множество, которое можно поместить целиком внутрь шара некоторого радиуса.

Функции многих переменных

Rn как пример метрического пространства

Сходимость в пространстве Rn

Открытые множества в Rn. Топология в Rn

Rⁿ как пример метрического пространства

Сходимость в пространстве Rⁿ

Открытые множества в Rⁿ. Топология в Rⁿ