Функции многих переменных

Определение. Если каждой точке x из некоторого открытого множества Ω точек пространства Rⁿ ставится в соответствие по известному закону некоторое число u∈ R, то говорят, что на множестве Ω задана функция u=u(x), или u=f(x₁,…,x_n).

В случае n=2 z=f(x,y), при n=3 — u=f(x,y,z). Если функция u=f(x) задана на множестве Ω, то это множество называется областью определения функции u=f(x). Число u, соответствующее данной точке M из множества Ω, будем называть частным значением функции в точке x. Совокупность \{u\} всех частных значений функции u=f(x) называется множеством всех значений этой функции.

Пример 1. 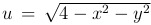. Областью задания этой функции является круг радиуса 2 с центром в начале координат, а множество значений представляют собой замкнутых отрезок 0≤ u≤ 2.

Пример 1. u=x²+y²+z². Областью задания этой функции является все евклидово пространство, а множеством значений — полупрямая u ≥ 0.

Определение. Пусть на Ω⊂Rⁿ определена функция u=f(x), u∈R. Рассмотрим Rⁿ⁺¹ — (n+1)-мерное евклидово пространство точек (x,y). Множество точек (x₁,…,x_n,f(x)) называется графиком функции f(x).

При n≥ 3 нет геометрической интерпретации.

Изучение графиков функции и самих функций в R² и R³ методом сечений. Здесь выделяются так называемые множества уровня.

Определение. Пусть функция f(x) определена на множестве Ω⊂ Rⁿ. Множество x∈ Rⁿ, удовлетворяющих уравнению

f(x₁, …, x₂) = c,

где c=const, называется множеством уровня функции f(x), соответствующих данному значению c.

При n=2 множество уровня называется линией уровня, при n=3 — поверхностью уровня, а при n>3 — гиперповерхностью уровня.

Предел и непрерывность функции нескольких переменных

Определение. Полное приращение функции двух переменных

z=f(x, y)

в точке M(x,y) определяется формулой

Δ z=f(x+Δ x, y+Δ y) - f(x,y),

а ее частные приращения (по x и y соответственно) в той же точке — формулами

Δ_x z=f(x+Δ x, y) - f(x, y); Δ_y z=f(x, y+Δ y) - f(x,y).

Аналогично определяются полное и частное приращения функции большего числа переменных.

Пусть дана функция дана функция u=f(x₁,…,x_n), областью определения которой является множество Ω∈ Rⁿ , и x⁰=(x₁⁰,…,x_n⁰).

Определение. Число a называется пределом функции u=f(x₁,…,x_n) в точке x⁰ (или при x→ x⁰), если f(x) определена в некоторой окрестности точки x⁰ (за исключением быть может самой точки x⁰) и для любой последовательности xⁿ → x⁰ .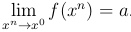

Определение. Число a называется пределом функции u=f(x₁,…,x_n) в точке x⁰ (или при x→ x⁰), если f(x) определена в некоторой окрестности точки x⁰ (за исключением быть может самой точки x⁰) и для любого числа ε>0 существует такое число δ>0, что для каждой точки x∈ Ω, удовлетворяющей условию

|x-x⁰|<δ,

выполняется неравенство

|f(x)-a|<ε.

Обозначение предела функции u=f(M) в точке M₀

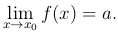
Если число a является пределом функции двух переменных u=f(x,y) в точке M₀(x₀,y₀), то употребляется также запись

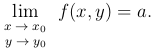
Определение. Будем писать 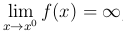определена в некоторой окрестности точки x⁰ (за исключением быть может самой x⁰) и для любого числа E>0 существует число δ>0 такое, что для любых x, для которых выполнено неравенство |x-x⁰|<δ, выполняется неравенство |f(x)|>E.

Определение. Под записью 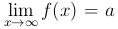понимается следующее. Для любого числа ε>0 существует число D=D(ε)>0 такое, что для любых x, для которых выполнено неравенство |x|>D, выполняется неравенство |f(x)-a|<ε.

Функция α=α(M) называется бесконечно малой в точке M₀, если

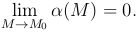
Теорема. Для того чтобы функция u=f(M) в точке M₀ имела предел, равный a, необходимо и достаточно, чтобы ее можно было представить в следующем виде:

f(M) = a+α(M),

где α(M) — бесконечно малая функция в точке M₀.

Теорема. Пусть функции f(x) и g(x) имеют в точке x⁰ предельные значения b и c. Тогда функции f(x)+g(x), f(x)-g(x), f(x)· g(x) и f(x)/g(x) имеют в точке x⁰ предельные значения, равные соответственно b+c, b-c, b· c, b/c.

Определение. Функция u=f(x) называется непрерывной в точке x₀, если она определена в некоторой точке x⁰ (включая саму эту точку) и предельное значение этой функции в точке x⁰ существует и равно частному значению f(A):

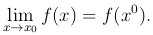
Необходимое и достаточное условие непрерывности функции u=f(x) в точке x⁰ выражается равенством

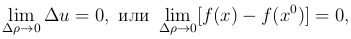
где Δρ=ρ(x,x⁰), Δ u = f(x)-f(x⁰).

Функция, непрерывная в каждой точке некоторого множества, называется непрерывной на этом множестве.

Теорема. Если функция u=f(x) определена и непрерывна на ограниченном замкнутом множестве, то она ограничена и достигает своего наименьшего и наибольшего значения.

Точки области определения функции, в которых функция непрерывна, называются точками непрерывности этой функции. Те точки области определения функции, в которых она не является непрерывной, называются точками разрыва этой функции.

Частные производные функции нескольких переменных

Определение. Частной производной функции нескольких переменных по одной из них в фиксированной точке называется предел отношения соответствующего частного приращения этой функции к приращению данной переменной, когда последнее стремится к нулю.

Для функции u=f(x₁, …, x_n) частная производная по x_j в точке x⁰=(x₁⁰, …, x_n⁰) определяется формулой

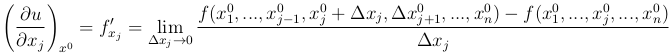
Таким образом, частная производная 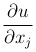есть обычная производная функции f(x₁, …, x_n), рассматриваемой как функция только от переменной x_j при фиксированных x₁, …, x_j-1, x_j+1, …, x_n.

Заметим, что 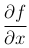— единый символ для обозначения частной производной функции f(x, y) по переменной x. Запись 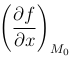означает, что частная производная вычислена в точке M₀(x₀, y₀).

Замечание. Пусть n=2. Тогда z=f(x,y) определяет поверхность в пространстве. Очевидно, что f′_x равна тангенсу угла наклона к оси x касательной к сечению этой поверхности плоскостью y=y₀ в точке с абсциссой x=x₀.

Если f(x₁, …, x_n) определена в G, то частные производные можно рассматривать как новые функции в G и снова можно дифференцировать.

Определение. Частными производными второго порядка (или вторыми частными производными) данной функции называются соответствующие частные производные от ее первых производных.

Для функции двух переменных u=f(x, y) распишем вторые частные производные. По определению имеем:

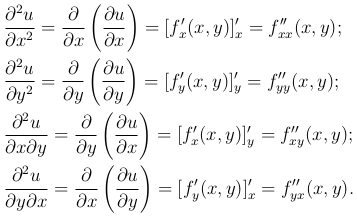
Вторые частные производные обозначаются также символами u″_xx, u″_xy, u″_yx, u″_yy. Производные u″_xy, u″_yx называются смешанными частными производными.

Теорема. Если функция u=f(x, y) и ее смешанные производные f″_xy, f″_yx определены в некоторой окрестности точки M₀(x₀, y₀), причем производные в этой точке непрерывны, то

f″_xy(x₀, y₀)=f″_yx(x₀, y₀).

Итак, если смешанные производные непрерывны, то они равны, то есть результат дифференцирования не зависит от порядка дифференцирования.