Дифференциалы высших порядков

Если x — независимая переменная, то (dx)′_x=0, так как dx не зависит от x. Тогда

Определение. Вторым дифференциалом от функции y=f(x) называется дифференциал от первого дифференциала

d²y = d(dy) = d(f′(x)dx) = (f′(x)dx)′dx = f″(x)dx².

Пусть нам известен дифференциал n-1-го порядка.

Определение. Дифференциалом n-го порядка называется дифференциал от дифференциала n-1-го порядка и выражается равенством:

dⁿy = f⁽ⁿ⁾(x)dxⁿ.

Если x=φ(t), то есть y=f(φ(t)). Тогда поскольку

dy = f′(x)dx,

то

d²y = d(dy) = d(f′(x)dx) = d(f′(x))dx + f′(x)d(dx) = f″(x)(dx)² + f′(x) d²x,

здесь d²x = φ″(t)dt².

Таким образом, доказали, что дифференциал второго порядка не обладает свойством инвариантности.

Дифференцирование функции, заданной параметрически

Пусть x и y заданы как функции некоторого параметра t: x=φ(t), y=ψ(t). При этом предположим, что функции φ(t) и ψ(t) имеют нужное число производных по параметру t в рассматриваемой области изменения этого параметра. Кроме того, будем считать, что функция x=φ(t) в окрестности рассматриваемой точки t=t₀ имеет обратную функцию t=φ^-1(x), ибо это позволяет рассматривать y как функцию аргумента x.

Рассмотрим вопрос о вычислении производной функции y=(x) по аргументу x.

В силу свойства инвариантности формы первого дифференциала мы можем записать равенства:

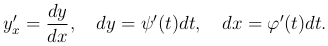
Из этих равенств сразу же вытекает, что

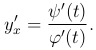
Дифференцирование функции, заданной неявно

Если дифференцируемая функция y=y(x) задана уравнением F(x,y)=0, то производная y′=y′(x) этой неявной функции может быть найдена из уравнения F′_x=0, где F=F(x,y) рассматривается как сложная функция от переменной x.

Основные теоремы о дифференцируемых функциям

Возрастание (убывание) функции в точке. Локальный экстремум

Рассмотрим функцию y=f(x), определенную всюду в некоторой окрестности фиксированной точки c.

Определение. Будем говорить, что функция y=f(x) возрастает в точке c, если найдется такая δ-окрестность точки c, в пределах которой

f(x)<f(c) при x<c и

f(x)>f(c) при x>c.

Определение. Будем говорить, что функция y=f(x) убывает в точке c, если найдется такая δ-окрестность точки c, в пределах которой

f(x)>f(c) при x<c и

f(x)<f(c) при x>c.

Определение. Будем говорить, что функция y=f(x) имеет в точке c локальный максимум (локальный минимум), если найдется такая δ-окрестность точки c, в пределах которой значение f(c) является наибольшим (наименьшим) среди всех значений f(x) этой функции.

Определение. Будем говорить, что функция y=f(x) имеет в точке c локальный экстремум, если эта функция имеет, в указанной точке либо локальный максимум, либо локальный минимум.

Теорема [достаточное условие возрастания или убывания функции в точке]. Если функция y=f(x) дифференцируема в точке c и ее производная в этой точке f′(c) положительна (отрицательна), то функция y=f(x) возрастает (убывает) в точке c.

Теорема [теорема Ферма]. Если функция y=f(x) дифференцируема в точке c и имеет в этой точке локальный экстремум, то f′(c)=0.

Замечание. Эта теорема выражает необходимое условие локального экстремума дифференцируемой в данной точке функции.

Теорема Ферма имеет очень простой геометрический смысл: она утверждает, что если в той точке кривой y=f(x), в которой достигается локальный экстремум, существует касательная к этой кривой, то эта касательная обязательно параллельна оси Ox.

Теорема о нуле производной

Теорема [теорема Ролля]. Пусть функция f(x) непрерывна на сегменте [a, b] и дифференцируема во всех внутренних точках этого сегмента. Пусть, кроме того, f(a)=f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что значение производной в этой точке f′(ξ) равно нулю.

Теорема Ролля имеет простой геометрический смысл: если крайние ординаты кривой y=f(x) равны, то согласно теореме Ролля на кривой y=f(x) найдется точка, в которой касательная к кривой параллельна оси Ox.

Формула конечных приращений (формула Лагранжа)

Теорема [теорема Лагранжа]. Если функция f(x) непрерывна на сегменте [a, b] и дифференцируема во всех внутренних точках этого сегмента, то внутри сегмента [a, b] найдется точка ξ такая, что справедлива формула

f(b)-f(a)=f′(ξ)(b-a).

Эту формулу называют формулой Лагранжа или формулой конечных приращений.

Для выяснения геометрического смысла теоремы Лагранжа заметим, что величина 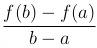есть угловой коэффициент секущей, проходящей через точки A(a, f(a)) и B(b, f(b)) кривой y=f(x), a f′(ξ) есть угловой коэффициент касательной к кривой y=f(x), проходящей через точку C(ξ, s(ξ)). Формула Лагранжа означает, что на кривой y=f(x) между точками A и B найдется такая точка C, касательная в которой параллельна секущей AB.

Часто бывает удобно записывать формулу Лагранжа в другом виде. Пусть f(x) удовлетворяет условиям теоремы. Зафиксируем любое x₀ из сегмента [a, b] и зададим ему приращение δ x произвольное, но такое, чтобы значение x₀+Δ x также лежало на сегменте [a, b]. Тогда, записывая формулу Лагранжа для сегмента, ограниченного точками x₀ и x₃+Δ x, будем иметь

f(x₀+Δ x)-f(x₀)=Δ x f′(ξ),

где ξ — некоторая точка, лежащая между x₀ и x₀+Δ x. Можно утверждать, что найдется такое (зависящее от Δ x) число θ из интервала 4<θ<1, что

ξ=x₀+θ Δ x.

Таким образом, получим формулу

f(x₀+Δ x)-f(x₀)=Δ x f′(x₀+θ Δ x),

где θ — некоторое число из интервала 0<θ<1. Формула Лагранжа в таком виде дает точное выражение для приращения функции через вызвавшее его произвольное конечное приращение Δ x аргумента. Этот вид формулы Лагранжа оправдывает термин «формула конечных приращений».

Обобщенная формула конечных приращений (формула Коши)

Теорема [теорема Коши]. Если каждая из двух функций f(x) и g(x) непрерывна на сегменте [a, b] и дифференцируема во всех внутренних точках этого сегмента и если, кроме того, производная g′(x) отлична от нуля всюду внутри сегмента [a, b], то внутри этого сегмента найдется точка ξ такая, что справедлива формула

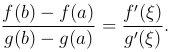
Эту формулу называют обобщенной формулой конечных приращений или формулой Коши.

Замечание 1. Формула Лагранжа является частным случаем формулы Коши при g(x)=x.

Замечание 2. В формуле Коши вовсе не обязательно считать, что b>a. Эта формула верна и при b<a.