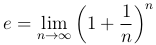Бесконечно большие и бесконечно малые последовательности

Определение. Последовательность {x_n} называется бесконечно большой, если для любого положительного числа A (сколь бы большим мы его не взяли) можно указать номер N=N(A) такой, что при n ≥ N все элементы x_n этой последовательности удовлетворяют неравенству

|x_n|>A.

Иногда формально бесконечно большие последовательности называют последовательностями, сходящимися к бесконечности. Это позволяет использовать для бесконечно большой последовательности {x_n} следующую символику

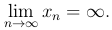
Если при этом все элементы бесконечно большой последовательности, начиная с некоторого номера, положительные (отрицательные), то используют следующую символику

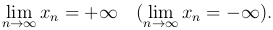
Определение. Последовательность {α _n} называется бесконечно малой, если для любого положительного числа ε (сколь бы малым мы его не взяли) можно указать номер N=N(ε) такой, что при n ≥ N все элементы α _n этой последовательности удовлетворяют неравенству

|α_n| < ε.

В соответствии с определением сходящейся последовательности всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число 0.

Число e

Применим теорему о существовании предела монотонной последовательности для доказательства существования предела последовательности {x_n}, элемент x_n которой определяется формулой

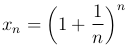
В силу теоремы достаточно доказать, что эта последовательность 1) является возрастающей; 2) ограничена сверху.

1) Применяя формулу бинома Ньютона, получим для x_n следующее выражение:

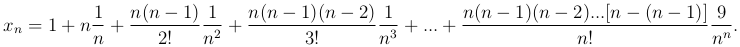
Это выражение перепишем в следующем виде:

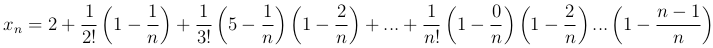
Совершенно аналогичным образом запишем элемент x_n+1:

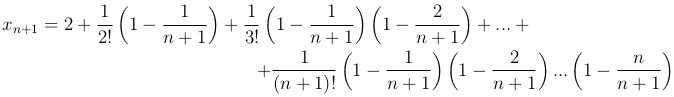
Поскольку 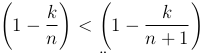для любого 0<k<n и x_n+1 содержит по сравнению с x_n лишний положительный элемент, то имеем

x_n < x_n+1,

т.е. последовательность {x_n} возрастающая.

2) Докажем теперь, что эта последовательность ограничена сверху. Заметим, что если каждую круглую скобку в правой части выражения для x_n заменить единицей, то указанная правая часть возрастет. Заметим далее, что для любого номера n ≥ 2 справедливо неравенство k! = 2 · 3 · … · k ≥ 2^k-1. Следовательно, получим

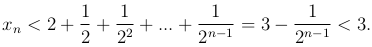
(Мы воспользовались формулой для суммы членов геометрической прогрессии.) Это неравенство доказывает ограниченность последовательности {x_n} сверху.

По основной теореме последовательность {x_n} имеет предел, который мы обозначим через e. следовательно, по определению