Бесконечно малые и бесконечно большие функции

Ради определенности будем рассматривать предел функции в точке a.

Определение. Функция α(x) называется бесконечно малой в точке a, если предел этой функции в точке a равен нулю.

Свойства бесконечно малых функций

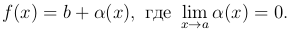
1) Если функция y=f(x) имеет предел в точке a, равный числу b, то

Обратное также верно: если выполнено это равенство, то .
2) Алгебраическая сумма конечного числа бесконечно малых функций при x → a есть бесконечно малая функция при x → a.
3) Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция. В частности, произведение двух бесконечно малых функций есть бесконечно малая функция и произведение бесконечно малой функции на постоянную есть бесконечно малая функция.

Введем теперь понятие бесконечно большой в данной точке a справа (или слева) функции.

Определение. Функция f(x) называется бесконечно большой в точке a справа (слева) функцией, если для любой сходящейся к a последовательности {x_n} значений аргумента, все элементы которой больше a (меньше a), соответствующая последовательность значений функции {f(x_n)} является бесконечно большой последовательностью, все элементы которой, начиная с некоторого номера, либо положительны, либо отрицательны.

Для бесконечно больших в точке a справа (слева) функций используется следующая символика:

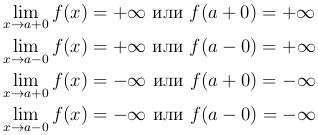
Остановимся на методике сравнения двух бесконечно малых в данной точке a функций. Пусть α(x) и β(x) — две функции, заданные для одних и тех же значений аргумента и обе являющиеся бесконечно малыми в точке a.

1) Говорят, что α(x) является в точке a бесконечно малой более высокого порядка, чем β(x) (имеет в точке a более высокий порядок малости, чем β(x)), если
2) Говорят, что α(x) и β(x) являются в точке a бесконечно малыми одного порядка (имеют в точке a одинаковый порядок малости), если
3) Говорят, что α(x) и β(x) являются в точке a эквивалентными бесконечно малыми, если

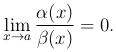
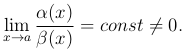
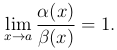
Для обозначения того, что α(x) является в данной точке бесконечно малой более высокого порядка, чем β(x), используют следующую запись:

α = o(β)

(читается: "a равно o малому от β").

Итак, символ o(β) обозначает любую бесконечно малую в данной точке a функцию, имеющую в этой точке более высокий порядок малости, чем бесконечно малая в той же точке функция β(x)). Из этого определения символа "o малое" вытекают следующие его свойства:

1. o(β)+o(β)=o(β), o(β)-o(β)=o(β);
2. если γ=o(β), то o(β)+o(γ)=o(β);
3. если α и β — любые две бесконечно малые в данной точке функции, то α · β=o(α) и α · β=o(β).

Теорема. Если α(x)∼α₁(x), β(x)∼β₁(x) при x → a и существует 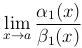, то существует 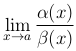, причем

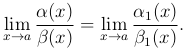
Аналогично сравниваются две бесконечно большие в данной точке a справа (или слева) функции.

Пусть A(x) и B(x) определены для одних и тех же значений аргумента и для определенности

1) Говорят, что A(x) имеет в точке a справа более высокий порядок роста, чем B(x), если функция A(x)/B(x) является бесконечно большой в точке a справа.
2) Говорят, что A(x) и B(x) имеют в точке a справа одинаковый порядок роста, если предел функции A(x)/B(x) при x → a+0 равен конечному числу, отличному от нуля.

Утверждение. Если функция α=α(x) стремится к нулю при x → a и не обращается в нуль, то функция y(x)=1/α(x) стремится к бесконечности.

Замечание. Аналогично определяются и сравниваются функции, бесконечно малые или бесконечно большие при x → ∞, а также при x → +∞ (соответственно при x → -∞).