Классификация точек разрыва функции

Устранимый разрыв.

Определение. Точка a называется точкой устранимого разрыва функции y=f(x), если предел функции f(x) в этой точке существует, но в точке a функция f(x) либо не определена, либо имеет частное значение f(a), отличное от предела f(x) в этой точке.

Пример. Например, функция

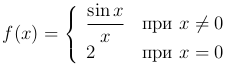
имеет в точке x=0 устранимый разрыв. Действительно, предельное значение этой функции в точке х=0 равно 1. Частное же значение равно 2.

Если функция f(x) имеет в точке a устранимый разрыв, то этот разрыв можно устранить, не изменяя при этом значений функции в точках, отличных от a. Для этого достаточно положить значение функции в точке a равным ее предельному значению в этой точке. Так, в рассмотренном выше примере достаточно положить f(0)=1 и тогда 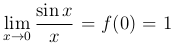, т.е. функция f(x) станет непрерывной в точке x=0.

Разрыв первого рода.

Определение. Точка a называется точкой разрыва, первого рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу правый и левый пределы

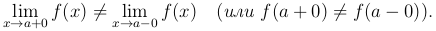
Приведем некоторые примеры.

Пример. Функция y=sgn x имеет в точке x=0 разрыв первого рода. Действительно, 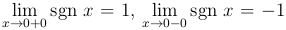и, таким образом, эти пределы не равны между собой.

Пример. Функция 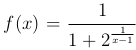, определенная всюду, кроме точки x=1, имеет в точке x=1 разрыв первого рода. В самом деле, .

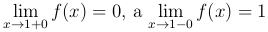Разрыв второго рода.

Определение. Точка a называется точкой разрыва второго рода, если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов или если хотя бы один из односторонних пределов бесконечен.

Пример. Функция f(x)=tg x, очевидно, имеет разрыв второго рода в каждой из точек x_k=π/2+π k, k=0, ± 1, ± 2,…, ибо в каждой такой точке

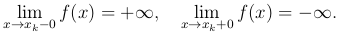
Пример. Функция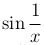 имеет разрыв второго рода в точке x=0, ибо в этой точке у нее не существует ни правого, ни левого пределов.

Непрерывность функции на отрезке

Определение. Функция, определенная на отрезке [a, b] и непрерывная в каждой его точке, называется непрерывной на этом отрезке.

При этом под непрерывность в точке a понимается непрерывность справа, а под непрерывностью в точке b — непрерывность слева.

Будем говорить, что функция y=f(x), определенная на множестве {x} достигает на нем своей верхней (нижней) грани 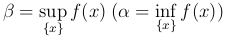, если существует такая точка x⁰∈{x}, что f(x⁰)=β (f(x⁰)=α).

Теорема [Вейерштрасса]. Всякая непрерывная на отрезке функция ограничена и достигает на нем своей верхней грани и своей нижней грани.

Теорема [Больцано-Коши]. Если функция y=f(x) непрерывна на отрезке [a, b] и f(a)=A, f(b)=B, то для любого C, заключенного между A и B, существует такая точка ξ∈[a, b], что f(ξ)=C.

Другими словами, непрерывная на отрезке функция, принимая какие-либо два значения, принимает и любое лежащее между ними значение.

Следствие. Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то на этом отрезке существует хотя бы одна точка, в которой функция обращается в нуль.

Следствие. Пусть функция y=f(x) непрерывна на отрезке [a, b] и 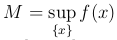, 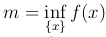. Тогда функция f(x) принимает все значения из отрезка [m, M] и только эти значения.

Таким образом, множество всех значений функции, заданной и непрерывной на некотором отрезке, представляет собой также отрезок.