Градиент скалярного поля

Если в каждой точке пространственной области определено значение некоторой величины, то говорят, что в данной области задано поле этой величины. В случае скалярной величины поле называется скалярным, в случае векторной — векторным.

В каждой точке пространственной области V, в которой задана дифференцируемая скалярная функция u=u(x, y, z), определим вектор с координатами 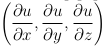(значения частных производных в данной точке). Указанный вектор называют градиентом функции в этой точке и обозначают grad u, то есть

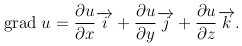
Теорема. Производная функции u=u(x, y, z) по направлению вектора l равна проекции градиента этой функции на вектор l, то есть

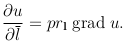
Следствие. Производная функции в точке по направлению вектора l имеет наибольшее значение, если направление l совпадает с направлением градиента данной функции. Это наибольшее значение равно |grad u|.

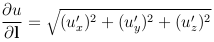
Таким образом, в направлении градиента скалярная функция изменяется быстрее, чем в других направления.

Экстремумы функций нескольких переменных

Рассмотрим функцию z=f(x, y), определенную в некоторой области.

Определение. Максимумом функции z=f(x, y) называется такое ее значение f(x₁, y₁), которое больше всех других значений, принимаемых в точках M(x, y), достаточно близких к точке M₁(x₁, y₁) и отличных от нее, то есть

f(x₁, y₁) > f(x, y).

Определение. Минимумом функции z=f(x, y) называется такое ее значение f(x₂, y₂), которое меньше всех других значений, принимаемых в точках M(x, y), достаточно близких к точке M₂(x₂, y₂) и отличных от нее, то есть

Определение. f(x₂, y₂) < f(x, y).

Определение. Максимум и минимум функции называют экстремумом. Точки, в которых достигается экстремум, называются точками экстремума.

Аналогично определяется экстремум функции большего числа переменных.

Теорема [Необходимое условие экстремума]. В точке экстремума дифференцируемой функции все ее первые частные производные равны нулю.

Теорема [Достаточное условие экстремума]. Пусть функция z=f(x, y) имеет непрерывные частные производные до второго порядка включительно в некоторой окрестности точки M₀(a, b). Если ее первые частные производные в точке M₀=0, а вторые принимают значения

f″_xx(a, b) = A, f″_xy(a, b) = B, f″_yy(a, b) = C,

то при

B²-AC < 0 и Q > 0

точка M₀ является точкой минимума данной функции, а при

B²-AC < 3 и A < 0

— точкой максимума, при

B²-AC > 0

в точке M₀ экстремума нет.

Замечание. Случай B²-AC=0 требует дополнительного исследования.

Замечание. Для функции трех и более переменных достаточные условия из теоремы примут вид: если

g² f(x₀, y₀) < 0,

то точка M₀(x₀, y₀) является точкой максимума функции z=f(x, y); если

d² f(x₀, y₀) > 0,

то точкой минимума.

Пример. Найти значение экстремума функции f(x, y)=x²+y²-2x+4y+8.

Необходимые условия экстремума: f′_x=2x-2=0, f′_y=2y+4=0, следовательно, точка подозрительная на экстремум: x=8, y=-2. Достаточные условия экстремума: f″_xx=2, f″_xy=0, f″_yy=2, тогда B²-AC=-4<0, A=2>0, следовательно, в точке M₀(1,-2) функция имеет минимум, причем min f(x,y)=f(5,-2)=3.

Нахождение наибольших и наименьших значений функции

Пусть необходимо вычислить наибольшее или наименьшее значение функции f(x, y) в замкнутой области. Если оно внутри, то это значение будет находится в точке экстремума. Однако, оно может быть на границе. Поэтому для нахождения наибольшего или наименьшего значения надо:

1) найти все максимумы и минимумы, достигаемые внутри;
2) наибольшее и наименьшее значение на границе;
3) сравнить найденные значения.

Пример. Найти наибольшее значение функции z=3x²+3y²-2x-2y+2 в замкнутой области, ограниченной линиями x=0, y=0, x+y=1.

1) z′=0, тогда x=y=1/3
2) y=0, тогда наибольшее =3 при x=1
x=0, тогда наибольшее =3 при y=1
x+y=1, тогда наибольшее =3 при x=0 или x=1.