Предел последовательности

Определение. Если каждому числу n натурального ряда чисел 1, 2, …, n, … ставится в соответствие по определенному закону некоторое вещественное число x_n, то множество занумерованных вещественных чисел

x₁, x₂, …, x_n, … (1)

мы будем называть числовой последовательностью или просто последовательностью.

Числа x_n будем называть элементами или членами последовательности (1). Сокращенно последовательность (1) будем обозначать символом {x_n}.

Например, символом {1/n} будем обозначать последовательность 1, 1/2, …, 1/n,…, а символ {1+(-1)ⁿ} будет обозначать последовательность 0, 2, 0, 2, …

Рассмотрим наряду с последовательностью (1) последовательность

y₁, y₂, …, y_n, … (2)

Определение. Назовем последовательность x₁+y₁, x₂+y₂, …, x_n+y_n, … (или {x_n+y_n}) суммой последовательностей (1) и (2); последовательность x₁-y₁, x₂-y₂, …, x_n-y_n, … (или {x_n-y_n}) — разностью последовательностей (1) и (2); последовательность x₁ · y₁, x₂ · y₂, …, x_n · y_n, … (или {x_n · y_n}) произведением последовательностей (1) и (2); и, наконец, последовательность x₁/y₁, x₂/y₂, …, x_n/y_n, … (или x_n/y_n) — частным последовательностей (1) и (2).

Замечание. Конечно, при определении частного последовательностей (1) и (2) необходимо требовать, чтобы все элементы последовательности (1) были отличны от нуля. Однако, если у последовательности {y_n} обращается в нуль лишь конечное число элементов, то частное {x_n/y_n} можно определить с того номера, начиная с которого все элементы y_n отличны от нуля.

Определение. Последовательность {x_n} называется сходящейся, если существует такое число a, что для любого положительного числа ε можно указать номер N=N(ε) такой, что при n ≥ N все элементы x_n этой последовательности удовлетворяют неравенству

x_n-a| < ε (3)

При этом число a называется пределом последовательности {x_n}.

Если последовательность {x_n} сходится и имеет своим пределом число a, то символически это записывается так:

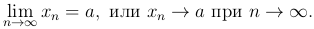
Замечание. Из определения сходящейся последовательности и ее предела сразу же вытекает, что удаление любого конечного числа элементов последовательности не влияет на сходимость этой последовательности и на величину ее предела.

Замечание. Последовательности, не являющимися сходящимися, принято называть расходящимися.

Неравенство |x_n-a|<ε равносильно неравенствам a-ε < x_n < a+ε.

Геометрический смысл определения предела: Число a является пределом последовательности {x_n}, если в любой его ε — окрестности, т.е. в интервале (a-ε, a+ε), содержатся почти все члены {x_n}, за исключением лишь конечного числа точек этой последовательности.

Утверждение. Последовательность имеет только один предел.

Теорема. Сумма, разность, произведение и частное двух сходящихся последовательностей {x_n} и {y_n} являются сходящимися последовательностями, причем для их пределов выполняются следующие равенства:

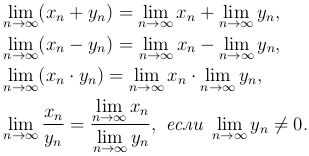
Утверждение. Если последовательность имеет предел, то она ограничена.

Теорема [Необходимое и достаточное условие существования конечного предела]. Числовая последовательность сходится к конечному пределу тогда и только тогда, когда для любого положительного числа ε существует номер N такой, что при всех n>N и любых натуральных m x_n-x_n+m<ε.

Определение. Последовательность {x_n} называется неубывающей (невозрастающей), если каждый последующий член этой последовательности не меньше (не больше) предыдущего, то есть если для всех номеров n справедливо неравенство

x_n ≤ x_n+1 (x_n ≥ x_n+1) (4)

Определение. Последовательность {x_n} называется монотонной, если она является либо неубывающей, либо невозрастающей.

Если в (4) имеет место строгое неравенство, то последовательность {x_n} называется возрастающей (убывающей). Возрастающие и убывающие последовательности называются также строго монотонными.

Теорема. Если неубывающая (невозрастающая) последовательность {x_n} ограничена сверху (снизу), то она сходится и имеет следующий предел:

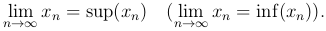
Другая формулировка теоремы: если монотонная последовательность {x_n} ограничена с обеих сторон, то она сходится.