Числовые множества

Совокупность рациональных и иррациональных чисел называется множеством всех действительных (или вещественных) чисел. Для любых двух действительных чисел a и b справедливо одно и только одно из соотношений: a<b, a=b, a>b. Действительные числа можно изображать точками на координатной оси. Между всеми действительными числами и всеми точками координатной оси устанавливается взаимно-однозначное соответствие. Поэтому множество действительных чисел иногда называют числовой прямой.

Если заданы два действительных числа a и b (a<b), то множество чисел, удовлетворяющих соотношениям a ≤ x ≤ b, называется замкнутым промежутком или отрезком [a, b], то есть [a, b]={x: a ≤ x ≤ b}.

Определение. Система числовых отрезков [a₁, b₁], [a₂, b₂], …, [a_n, b_n], …, a_n ∈ R, b_n ∈ R, n=1, 2, … называется системой вложенных отрезков, если a₁ ≤ a₂ ≤ … ≤ a_n ≤ … ≤ b_n ≤ … ≤ b₂ ≤ b₁, т.е. если каждый следующий отрезок [a_n+1, b_n+1] содержится в предыдущем [a_n, b_n].

Теорема [Принцип вложенных отрезков]. Всякая система вложенных отрезков, длина которых стремится к нулю, имеет единственное число, которое принадлежит всем отрезкам данной системы.

Если a<b, то множество действительных чисел (a,b)={x: a< x<b} называется открытым промежутком, или интервалом.

Всякий интервал (x-ε, x+ε), где ε>0 называется ε-окрестностью (или просто окрестностью) точки x на числовой прямой. Обозначение: O(x, ε).

Предельной точкой множества называется точка, в любой окрестности которой содержится, по крайней мере, одна точка данного множества, отличная от нее самой. Любое действительное число является предельной точкой для множества всех рациональных чисел.

Множество всех действительных чисел называют бесконечным промежутком и обозначают (-∞, ∞). Считают по определению, что -∞<x<∞ для любого действительного числа x.

Определение. Множество X действительных чисел x называется ограниченным сверху, если существует такое число b, что x ≤ b для всех x ∈ X. В этом случае говорят, что число b ограничивает сверху множество X.

Множество X действительных чисел x называется ограниченным снизу, если существует такое число a, что x ≥ a для всех x ∈ X. В этом случае говорят, что число a ограничивает снизу множество X.

Множество X действительных чисел, ограниченное сверху и снизу, называется ограниченным; то есть множество X ограничено, если существуют числа a и b такие, что a ≤ x ≤ b для всех x ∈ X.

Определение. Число M называется верхней гранью числового множества X, если:

1) x ≤ M для всех x ∈ X;
2) для любого числа ε>0 существует такое x_ε ∈ X, что x_ε > M-ε.

Верхняя грань множества X обозначается через sup X, или .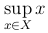

Определение. Число m называется нижней гранью числового множества X, если: 1) x ≥ m для всех x ∈ X; 2) для любого числа ε>0 существует такое x^ε ∈ X, что x^ε > m+ε. Нижняя грань множества X обозначается через inf X, или 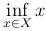. Верхняя и нижняя грани множества могут принадлежать или не принадлежать этому множеству. Если некоторое множество X действительных чисел не ограничено сверху, то полагают по определению sup X=+∞; если множество не ограничено снизу, полагают inf X=-∞.

Теорема. У всякого множества действительных чисел верхняя (нижняя) грань единственна.