Полный дифференциал функции нескольких переменных

Рассмотрим функцию двух переменных z=f(x, y) и ее полное приращение в точке M₀(x₀, y₀)

Δ z = f(x₀+Δ x, y₀+Δ y) - f(x₀, y₀).

Определение. Если существуют числа P и Q такие, что полное приращение можно представить в виде

Δ z = PΔ x + QΔ y + ε Δρ,

где 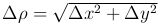и ε→ 0 при Δρ→ 0, то выражение PΔ x + QΔ y называется полным дифференциалом функции z=f(x,y) в точке M₀(x₀,y₀).

В этом случае полное приращение функции состоит из двух частей: первая часть PΔ x + QΔ y является линейной относительно Δ x и Δ y, вторая — бесконечно малой высшего порядка по сравнению с .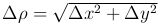

Полный дифференциал функции z=f(x,y) обозначается через dz, то есть

dz = PΔ x+QΔ y.

Функция, имеющая полный дифференциал в данной точке, называется дифференцируемой в этой точке.

Теорема. Если u=f(M) дифференцируема в точке M₀, то она в ней непрерывна.

Замечание. Из непрерывности функции двух переменных не следует ее дифференцируемость.

Пример. 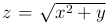непрерывна в (0,0), но не имеет частной производной 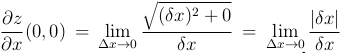— не существует. Аналогично не существует частной производной по y. Следовательно, функция не дифференцируема.

Теорема [необходимое условие дифференцируемости]. Если z=f(x,y) дифференцируема в точке M₀, то она имеет в этой точке частные производные по x и y, причем

f′_x(x₀,y₀) = P, f′_y(x₀, y₀) = Q.

Замечание. Из существования частных производных не следует дифференцируемость. Пример:

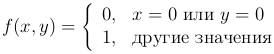
Имеем 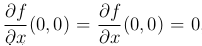, но функция не является непрерывной, следовательно не является дифференцируемой.

Теорема [достаточное условие дифференцируемости]. Если первые частные производные функции z=f(x,y) определены в некоторой окрестности точки M₀(x₀,y₀) и непрерывны в самой точке M₀, то данная функция имеет полный дифференциал в этой точке.

Замечание. Имеем

Δ z = f′_x(x₀, y₀)Δ x + f′_y(x₀, y₀)Δ y + ε Δρ,

где ε→ 0 при Δρ→ 0. Следовательно,

f(x₀+Δ x,y₀+Δ y) - f(x₀,y₀) ≈ f′_x(x₀,y₀)Δ x + f′_y(x₀,y₀)Δ y

или

f(x₀+Δ x, y₀+Δ y) ≈ f(x₀,y₀) + f′_x(x₀, y₀)Δ x + f′_y(x₀, y₀)Δ y.

Эта формула применяется в приближенных вычислениях.

При фиксированных Δ x и Δ y полный дифференциал является функцией переменных x и y:

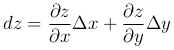
Положим dx=Δ x, dy=Δ y и назовем эти величины дифференциалами независимых переменных.

Тогда получим формулу

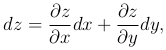
то есть полный дифференциал функции равен сумме произведений первых частных производных на соответствующие дифференциалы аргументов.

Аналогично определяется и выражается полный дифференциал функции трех переменных. Если u=f(x, y, z) и существуют числа P, Q, R такие, что

Δ u = PΔ x+QΔ y+RΔ z+εΔρ, ε→ 0 при δρ→ 0,

то полным дифференциалом называется выражение

du = PΔ x+QΔ y+RΔ z.

Если первые частные производные этой функции непрерывны, то

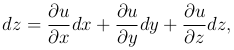
где dx=Δ x, dz=Δ z, dz=Δ z.

Определение. Полным дифференциалом второго порядка некоторой функции называется полный дифференциал от ее полного дифференциала.

Если z=f(x,y), dz=z′_xdx+z′_ydy, то

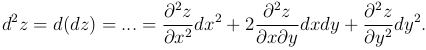
Касательная плоскость и нормаль к поверхности

Рассмотрим поверхность S, заданную уравнением

z=f(x, y).

Пусть f(x, y) имеет частные производные в некоторой области. Рассмотрим M₀(x₀, y₀).

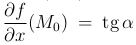— угловой коэффициент касательной в точке M₀ к сечению поверхности плоскостью y=y₀, то есть к линии z=f(x,y₀). Касательная к этой линии имеет вид:

z-z₀=f′_x(x₀, y₀)(x-x₀), y=y₀.

Аналогично, сечение плоскостью x=x₀ дает уравнение

z-z₀=f′_y(x₀, y₀)(y-y₀), x=x₀.

Плоскость, содержащая обе эти прямые, имеет уравнение

z-z₀=f′_x(x₀, y₀)(x-x₀)+f′_y(x₀, y₀)(y-y₀)

и называется касательной плоскостью к поверхности S в точке P₀(x₀, y₀, z₀).

Отметим, что уравнение касательной плоскости можно переписать в виде

z-z₀=df.

Таким образом, геометрический смысл полного дифференциала: дифференциал в точке M₀ для приращения (x-x₀, y-y₀) есть приращение аппликаты точки касательной плоскости к поверхности z=f(x,y) в точке (x₀, y₀) для тех же приращений.

Касательная плоскость имеет вектор нормали в точке (x₀, y₀, z₀) — \vec{n}=(f′_x(x₀, y₀), f′_y(x₀, y₀), -1). Прямая, проходящая через точку P₀ и имеющая направляющий вектор \vec{n}, называется нормалью к поверхности z=f(x,y) в данной точке. Ее уравнения:

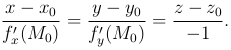
Дифференцирование сложных функций

Пусть дана дифференцируемая функция z=F(v, w), аргументы которой являются дифференцируемыми функциями переменных x и y:

v=v(x, y), w=w(x, y).

Если при этом функция

z=F(v(x, y), w(x, y))=\Phi(x, y)

имеет смысл, то она называется сложной функцией от x и y.

Теорема. Частные производные z′_x, z′_y сложной функции существуют и выражаются формулами

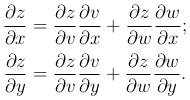
Если v и w — дифференцируемые функции одной переменной t, то есть

v=v(t), w=w(t),

и имеет смысл функция

z=F(v(t), w(t))=f(t),

то ее производная выражается формулой

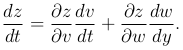
Эта производная называется полной производной.

Если задана дифференцируемая функция

u=F(ξ, η, ζ),

аргументы которой ξ=ξ(t), η=η(t), ζ=ζ(t) — дифференцируемые функции переменной t и функция

u=F(ξ(t), η(t), ζ(t))

имеет смысл, то ее полная производная находится по формуле

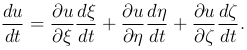
Дифференцирование неявных функций

Теорема. Если y=y(x) — непрерывная функция, заданная уравнением

F(x, y)=0,

где F(x,y), F′_x(x,y), F′_y(x,y) — непрерывные функции в области, содержащей точку M(x,y), в которой F′_y(x,y)≠ 0, то производная функции y=y(x) в соответствующей точке существует и выражается формулой

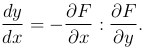
Если z=z(x, y) — функция, определяемая уравнением

F(x, y, z)=0,

где F(x, y, z), F′_x(x,y, z), F′_y(x, y, z), F′_z(x, y, z) — непрерывные функции в области, содержащей точку M(x, y, z), в которой F′_z(x, y, z)≠ 0, то

Производная по направлению

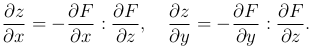
Рассмотрим функцию u=u(x, y, z), определенную и дифференцируемую в некоторой области S. Из точки M₀(x₀, y₀, z₀) этой области отложим вектор 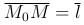, образующий с координатными осями углы α, β, γ соответственно. Предположим, что точка M(x₀+Δ x, y₀+Δ y, z₀+Δ z) также принадлежит области S.

Полное приращение функции u=u(x, y, z) можно представить в виде

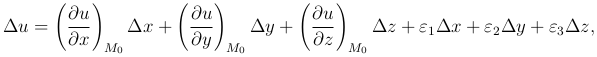
где ε_i→ 0 (i=1, 2, 3) при Δ x→ 0, Δ y→ 0, Δ z→ 0.

Разделим это равенство на :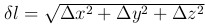

Поскольку

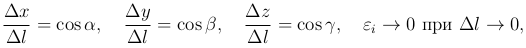
то

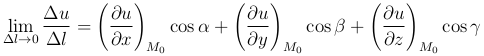
— производная функции u=u(x, y, z) в точке M₀(x₀, y₀, z₀) по направлению вектора 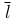обозначается символом 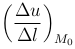. Следовательно,