Переменные величины и функции

Понятие функции. Обычно в приложениях имеют дело не с одной переменной величиной, а с несколькими связанными между собой величинами. Рассмотрим пример. Для описания состояния 1 кг воздуха требуются три переменные величины: давление p (размерность кг/м³), под которым он находится; занимаемый им объем v (м³) и его температура t (^o К). При постоянной температуре (для определенности положим t=273 К, это соответствует 0^o C) увеличение давления p приведет к уменьшению объема v. Давление p мы можем менять произвольно (в определенном промежутке, в данном случае p не может быть отрицательным), поэтому p можно назвать независимой переменной. Для каждого значения давления газ будет занимать вполне определенный объем, т.е. величина объема зависит от величины давления, а значит объем можем назвать зависимой переменной. Данную зависимость описывает закон Бойля-Мариотта. Для нашего случая этот закон представляет зависимость v и p в виде уравнения:

v = 273·29,27/p.

Переменная величина v называется функцией независимой переменной p.

Определение (функции). Величина y называется функцией независимой переменной x, если любому определенному значению x (из множества ее возможных значений) соответствует определенной значение y.

Выбор зависимой и независимой переменной определяется удобством. Например, если в нашем примере мы можем менять объем воздуха v, то v будет независимой переменной, а ее функцией будет давление p:

p = 273·29,27/v.

Количество переменных может быть любым. Например, если температура может меняться, то закон Бойля-Мариотта меняется на закон Клайперона:

pv = 29,27(273+t).

Поскольку в последнем выражении из трех величин мы можем изменять только две (третья определяется уравнением), то уравнение содержит две независимые переменные, а функция выражается через них.

Приведем привер из геометрии. Площадь треугольника S выражается через длины сторон a, b, c и полупериметр p по формуле Герона

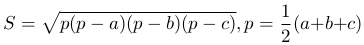
Стороны a, b и c можно менять произвольно, лишь бы любая сторона была бы больше разности и меньше суммы двух других сторон (иначе нельзя будет образовать треугольник). Тогда стороны a, b и c будут независимыми переменными, а площадь S — функцией от них.

Зная площадь треугольника S и любые две стороны a и b с помощью формулы

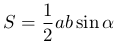
где α — угол между сторонами a и b, мы можем вычислить α. Здесь S, a и b — независимые переменные, а α — функция. Поскольку sin α — ограниченная единицей функция, то требования к независимым переменным определяют неравенства:

sin α = 2S / (ab) ≤ 1.

В данном примере, для заданых значений независимых переменных равенству sin &alpha = 2S / (ab) удовлетворяют два значения функции, соответствующие острому и тупому угол α.

Таким образом, функция может быть многозначной.

Аналитический способ задания функции. Законы природы, связывающие одни явления с другими, устанавливают функциональную зависимость между величинами.

Основные способы задания функциональных зависимостей следующие:

аналитический, когда величины связаны с помощью уравнения арифметическими операциями (сложение, вычитание, умножение, деление, логарифмирование и т. д.). Аналитические функции используются при теоретическом изучении явлений, т.е. когда собраны основные предпосылки (например наблюдением или экспериментом) используется математический анализ для установления зависимостей величин в виде формулы. Если функция (зависимая переменная) выражается через независимые переменные, то говорят, что функция аналитически задана явно. Например, приведенная выше формула Герона или формулы состояния газа.
табличный, когда значения наиболее используемых функций вычисляется заранее для наборов независимых переменных и результат вычислений записывается в таблицу. Простейший пример — таблица умножения, более сложные примеры — таблицы специальных функций. Если необходимо получить значение функции для переменных, которые в таблице не указаны, то можно воспользоваться интерполяцией. Часто табличный способ является основным, если функциональная зависимость неизвестна. Например, результаты экспериментов первоначально записываются в виде таблицы, а уже на ее основе, используя математический аппарат, стремятся определить функциональную зависимость.
графический или геометрический способ позволяет отображать значение переменной отрезком, а не числом.

Если нет возможности записать формулу, которая выражает функцию через независимые переменные, пишут кратное обозначение формулы:

y=f(x).

Эта запись означает, что y является функцией независимой переменной x, а f — символический знак зависимости y от x. Для разных функций используются разные символические знаки, например, phi(x), F(x) и т.д.

Символическая запись для функции нескольких переменных:

v=F(x, y, z)

означает, что v есть функция зависящая от x, y и z.

Если задать конкретные значения независимым переменным, по получим частное значение функции. Например, для функции

y = x² + 2x - 3

для x = 1 частное значение функции будет y=1²+2·1-3 = 0.

Функцию можно определить различными аналитическими формулами на различных промежутках независимой переменной. Например, y=x на промежутке (0, 5) и y=10—x на промежутке (5, 10). На всей области определения x в промежутке (0, 10) функция y определена.

Определение (неявная функция). Функция называется неявной, если нет выражения этой функции, через независимые переменные, а имеется только уравнение связывающее ее и независимые переменные.

Пример для формулы площади треугольника, где функция α неявно зависит от переменных a, b и S:

a b sin α = 2S

Неявная функция v от нескольких независимых переменных x, y и z определяется уравнением

F(x, y, z, v) = 0.

Если преобразовать это уравнение к виду

v=Φ(x, y, z),

т.е. к явному виду, то мы можем вычислить значения функции v.

Использованная литература

В. И. Смирнов. Курс высшей математики. Том 1. М.: Наука. 1974.