Функции и числа
Линейная функция
Простейшей функцией, имеющей тем не менее множество важных приложений, является линейная функция представляющая собой двучлен первой степени:
y = a x + b, (1
)
где a и b вещественные числа. Проведем исследование этой функции. Для начала положим в уравнении (1) b=0:
y = a x, (2)
Переменная y прямо пропорциональна переменной x, поэтому число a называется коэффициентом пропорциональности. Кривая (2) проходит через начало координат, поскольку x=0 и y=0 удовлетворяют уравнению (2).
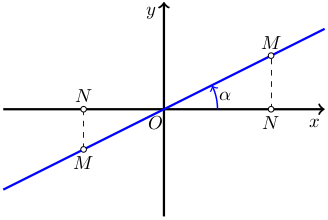
Рис. 1
Из рисунка 1 видно, что для любой точки M, принадлежащей линейной функции, отношение ординаты y (отрезок NM) этой точки к ее абсциссе x (отрезок ON) есть постоянная величина a равная тангенсу угла α, следовательно геометрическое место точек M, есть прямая, проходящая через начало координат и образующая угол α (или π+α) к оси OX. Угол α отсчитывается от оси OX до прямой против часовой стрелки. Коэффициент a называется угловым коэффициентом. Если a<0, то соответствующий угол больше 90° и прямая выглядит, как на рисунке 2.
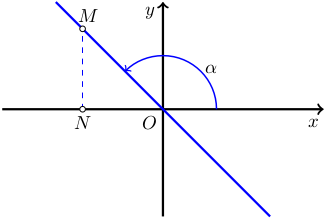
Рис. 2
Вернемся к общему виду уравнения (1). Если подставить в уравнение значение x=0, то получим y=b, т.е. прямая пересекает ось OY в ординате b (если b>0, то пересечение лежит над осью OX, а при b< 0, под ней). Коэффициент b называют начальной ординатой.
Определение. Графиком линейной функции (1) является прямая, коэффициент a которой равен тангенсу угла между осью OX и прямой, а коэффициент b равен отрезку отсекаемому прямой от оси OY считая от начала координат O.
В частном случае a=0, тангенс соответствует углу 0°, т.е. прямой параллельной оси OX и отстоящей от нее на расстоянии b. Значение функции y будет постоянным и равным b:
y = b.
Определение. Приращением независимой переменной x при переходе от начального значения x1 к конечному x2 называется разность между конечным и начальным значениями:
Δ x = x2 - x1.
Соответствующим приращением функции y=f(x) называется разность между конечным и начальным значением функции:
Δ y = y2 — y1 = f(x2) —f(x1).
Отметим, что приращение может быть как положительным, так и отрицательным или нулевым.
Рассмотрим уравнение линейной функции для двух значений переменной x:
y1 = ax1 + b и y2 = ax2 + b.
Почленно вычитая из второго выражения первое получим
y2 — y1 = a (x2 — x1) или Δy = a Δx. (3)
Свойство линейной функции. Свойством линейной функции y=ax+b является пропорциональность приращения функции (y2 — y1) приращению независимой переменной (x2 — x1), с коэффициентом пропорциональности равном a (угловому коэффициенту или уклону графика функции).
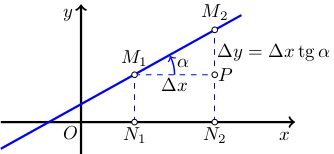
Рис. 3
На рисунке 3 это свойство показано графически. Приращение независимой переменной соответствует отрезок M1P, приращению функции — M2P. Из треугольника M1PM2 вытекает соотношение (3), где a=tg α.
Предположим, что некая функция обладает указанным выше свойством пропорциональности приращению независимой переменной. Тогда из соотношения (3)
y2 = a (x2 — x1) + y1.
Будем считать x2 независимой переменной функции y2, а значения x1 и y1 фиксированными. Перепишем последнее соотношение в виде:
y2 = ax2 + (y1 — ax1).
Выражение в скобках является фиксированным числом, обозначим его через b. Переобозначим функцию y2 через y, а независимую переменную x2 через x. Окончательно получим
y = ax + b.
Следовательно, всякая функция обладающая свойством пропорциональности приращению независимой переменной, есть линейная функция y = ax + b с коэффициентом пропорциональности a.
Важным приложением данного свойства является то, что любой закон природы, в котором имеет место пропорциональность исследуемых величин, описывается линейной функцией и изображается ее графиком, прямой линией.
Пример: равномерное движение. Рассмотрим пример из механики — равномерное движение объекта. Если точка M движется по некоторому пути (траектории), то ее положение определяется расстоянием от некоторой точки M0 на этой траектории до точки M длиной дуги M0M. Пройденный путь s является функцией независимой переменной времени t и мы можем построить график функциональной зависимости (рисунок 4, синяя линия) s=f(t).
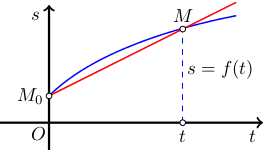
Рис. 4
Движение называется равномерным, если путь, проходимый точкой за любой промежуток времени пропорционален этому промежутку:
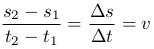(4)
При этом коэффициент пропорциональности v называется скоростью движения есть величина постоянная v=const.
Пусть на начальный момент времени t=0 был пройден путь s0, тогда, из соотношения (4), уравнение графика равномерного движения будет иметь вид:
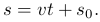
Это уравнение есть уравнение прямой, угловой коэффициент которой равен скорости движения, а начальная ордината s0 равная значению s в начальный момент времени t=0 (рисунок 4, красная линия).
Использованная литература