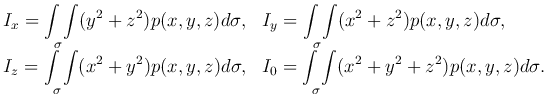Приложения интеграла

Приложения двойного интеграла

Как мы уже знаем, объем тела и масса пластинки вычисляются по формулам:

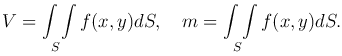
С помощью двойного интеграла можно вычислить площадь плоской области. Действительно, положив в первой из этих формул f(x,y) ≡ 1, получим V = 1 · S = S, то есть

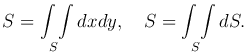
Центр тяжести. Пусть в точке M₁(x₁,y₁), M₂(x₂,y₂), …, M_n(x_n,y_n) сосредоточены соответственно массы m₁, m₂, …, m_n. Центр тяжести данной системы материальных точек находится в точке, координаты которой выражаются формулами:

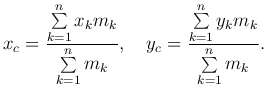
Найдем координаты центра тяжести пластинки, занимающей в плоскости Oxy некоторую область S. Пусть p = p(x,y) - плотность этой пластинки в точке M(x,y). Разобьем область на элементарные области (ΔS_k) (k=1,…,n), площади которых обозначим через ΔS_k соответственно. Будем считать, что плотность в каждой области (ΔS_k) постоянна и равна p_k=p(x_k,y_k) и вся ее масса m_k=p_kΔS_k=p(x_k,y_k)ΔS_k сосредоточена в точке M_k(x_k,y_k).

Координаты центра тяжести полученной системы материальных точек M_k(x_k,y_k) выражаются формулами:

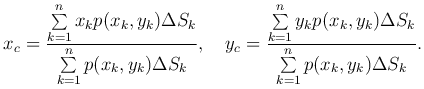
Эти формулы приближенно выражают координаты центра тяжести пластинки.

Обозначим через d_k диаметр области (ΔS_k) (k=1,…,n). Пусть &lambda_n - наибольший из этих диаметров. Перейдем к пределам этих сумм при λ_n→0. Эти пределы равны соответствующим двойным интегралам.

Следовательно, координаты центра тяжести рассматриваемой пластинки определяются формулами

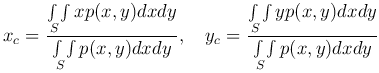
или

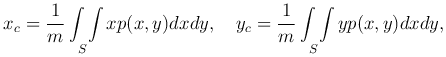
где m - масса пластинки.

Двойные интегралы

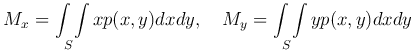
называются статистическими моментами пластинки S относительно осей Oy и Ox соответственно.

Если пластинка однородна, то есть p(x,y) =const, то получим

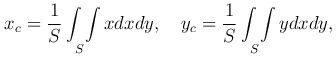
где S - площадь области S.

Момент инерции.

Определение. Моментом инерции I_O материальной точки M с массой m относительно точки O называется произведение массы на квадрат расстояния r=ρ(O,M) между данными точками, то есть

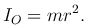
Определение. Моментом инерции системы материальных точек M₁(x₁,y₁), M₂(x₂,y₂), …, M_n(x_n,y_n) с массами m₁, m₂, …, m_n относительно точки O называется сумма моментов инерции всех этих точек:

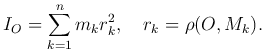
Аналогично определяется момент инерции системы указанных материальных точек относительно оси Ou:

где r_k - расстояние от точки M_k до оси Ou.

Определим момент инерции пластинки S с плотностью p=p(x,y) относительно точки O - начала прямоугольной декартовой системы координат.

Разбивая эту область на n элементарных областей (ΔS_k) (k=1,…,n) и считая, что масса m_k=p(x_k,y_k)ΔS_kобласти (ΔS_k) сосредоточена в точке M_k(x_k,y_k)∈(ΔS_k), получаем систему n материальных точек. Так как

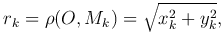
то момент инерции этой системы относительно точки O выразится так:

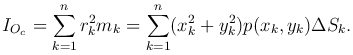
Определение. Моментом инерции пластинки относительно начала координат называется предел суммы I_Oc при λ_n→0, где λ_n - наибольший из диаметров d_k областей (ΔS_k) (k=1,…,n):

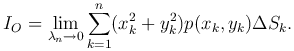
или

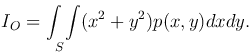
Моменты инерции этой пластинки относительно координатных осей Ox и Oy определяются формулами:

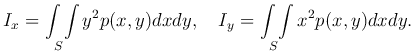
Отметим, что получили I_O=I_x+I_y.

Приложения тройного интеграла

Формулы для вычисления массы материальной области по заданной объемной плотности p=p(x,y,z) и объема тела:

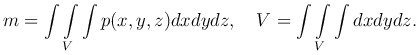
Тройной интеграл применяется также при вычислении координат центра тяжести C(x₀,y₀,z₀) материальной области V, в которой распределено вещество с объемной плотностью p=p(x,y,z). По аналогии с двойным интегралом получим

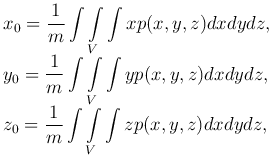
где m - масса соответствующей области, определяемая формулой

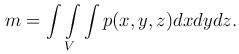
Моменты инерции материальной области V относительно координатных осей Ox, Oy, Oz и начала координат определяется соответственно формулами

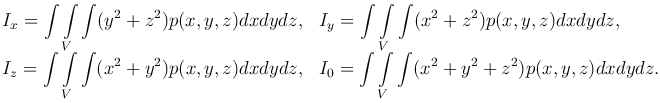
Приложения криволинейных интегралов

Масса материальной дуги. Если p=p(x,y,z) - плотность вещества, распределенного по дуге AB, то масса этой дуги:

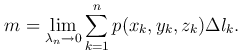
Следовательно,

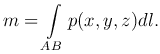
Длина дуги линии. Если p(x,y,z)≡1, тогда масса дуги AB m=1·l, m=l. Следовательно,

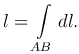
Центр тяжести материальной дуги. Если p=p(x,y,z) - плотность вещества, распределенного по дуге AB, то прямоугольные декартовы координаты ее центра тяжести C₀(x₀,y₀,z₀) выражаются формулами:

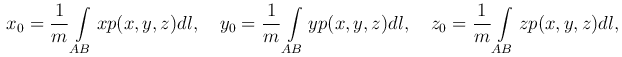
где m - масса дуги.

Моменты инерции материальной дуги. Моменты инерции материальной дуги AB, по которой распределено вещество с плотностью p=p(x,y,z), относительно координатных осей и начала координат:

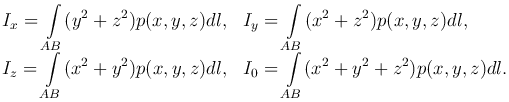
Работа переменной силы. Если F=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k - переменная сила, совершающая работу W вдоль криволинейного пути AB, и функции P(x,y,z), Q(x,y,z), R(x,y,z) - непрерывны, то

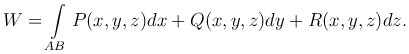
Приложения интегралов по поверхности

Масса материальной поверхности m, по которой распределено вещество с плотностью p=p(x,y,z), распределяется формулой:

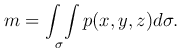
Площадь поверхности. Если p(x,y,z)≡1, тогда m=1·σ=σ. Следовательно,

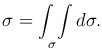
Центр тяжести материальной дуги. Если p=p(x,y,z) - плотность вещества, распределенного по поверхности σ, то прямоугольные декартовы координаты ее центра тяжести M₀(x₀,y₀,z₀) выражаются формулами:

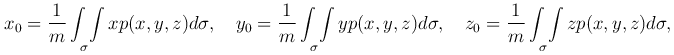
где m - масса поверхности. Для однородной поверхности (p≡const) имеем:

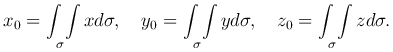
Моменты инерции материальной поверхности. Моменты инерции материальной поверхности σ, по которой распределено вещество с плотностью p=p(x,y,z), относительно координатных осей и начала координат: