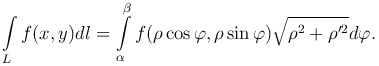Интегральное исчисление
Интегральное исчисление
 Криволинейный интеграл первого рода
Криволинейный интеграл первого рода
Рассмотрим пространственную кусочно--гладкую кривую, ограниченную точками A и B (рис. 1) и определенную на ней непрерывную функцию u=f(x,y,z).
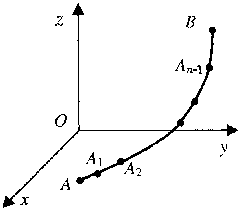
Рис. 1
Разобьем дугу AB на n элементарных дуг Ak-1Ak (k=1,…,n; A0=A, An=B), длины которых обозначим через Δlk соответственно. На каждой элементарной дуге Ak-1Ak выберем произвольную точку Mk(xk,yk,zk). Значение функции в этой точке f(xk,yk,zk) умножим на длину дуги Δlk и составим сумму всех таких произведений:
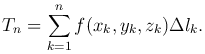
Эта сумма называется интегральной суммой для функции f(x,y,z) по длине дуги кривой AB.
Обозначим через 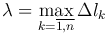 и перейдем к пределу при λ→0.
и перейдем к пределу при λ→0.
Определение. Если существует предел интегральной суммы Tn при λ→0, то он называется криволинейным интегралом первого рода (или интегралом от функции по длине дуги).
Таким образом, по определению
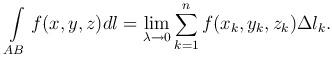
Теорема. Предел интегральной суммы Tn при λ→0 существует, если функция u=f(x,y,z) непрерывна на дуге AB.
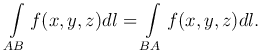
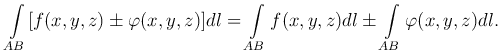
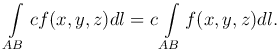
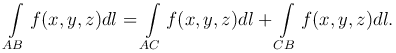
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла.
Если пространственная кривая L=AB задана параметрическими уравнениями
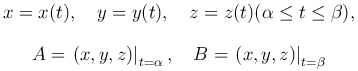
и x(t), y(t), z(t) - непрерывно дифференцируемые функции, то
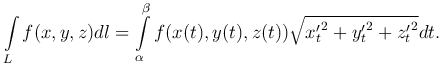
В частности, если кривая L лежит в плоскости Oxy (z=0), то
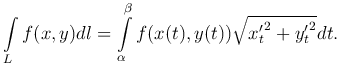
Если плоская кривая задана уравнением y=y(x), где a≤x≤b, y(x) - непрерывно дифференцируемая функция, то
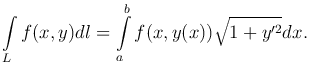
Если плоская кривая задана уравнением в полярных координатах ρ=ρ(φ), где α≤φ≤β, ρ(φ) - непрерывно дифференцируемая функция, то