Криволинейный интеграл второго рода

Рассмотрим дугу AB пространственной линии и укажем на ней направление от A к B. Пусть на этой дуге определена и непрерывна вектор-функция

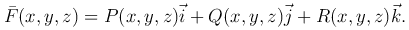
Разобьем дугу AB на n элементарных дуг A_k-1A_k (k=1,…,n; A=A₀, B=A_n), на дуге A_k-1A_k выберем произвольную точку M_k(x'_k,y'_k,z'_k). Обозначим декартовы координаты точек A_k(x_k,y,sub>k,z_k), тогда проекции дуги A_k-1A_k на координатные оси выразятся формулами:

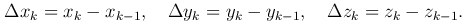
Значения функций P(x,y,z), Q(x,y,z), R(x,y,z) в точке M_k(x'_k,y'_k,z'_k) умножим соответственно на Δx_k, Δy_k, Δz_k и сложим:

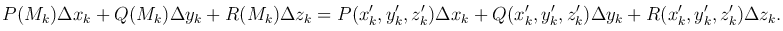
Составим сумму всех таких выражений:

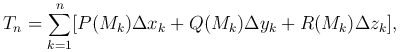
которая называется интегральной суммой по координатам для вектор-функции .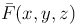

Замечание. Отличие интегральной суммы по длине дуги от интегральной суммы по координатам состоит в том, что значение функции в фиксированной точке элементарной дуги умножается не на длину этой дуги, а на ее проекцию на соответствующую координатную ось.

Пусть 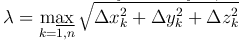и перейдем к пределу при λ→0.

Определение. Если существует предел интегральной суммы T_n при λ→0, то он называется криволинейным интегралом второго рода от вектор-функции 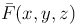и обозначается

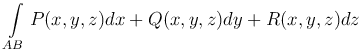
или

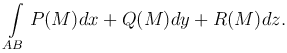
Итак, по определению

Свойства криволинейного интеграла второго рода

1. При перемене направления интегрирования криволинейный интеграл второго рода меняет лишь знак, поскольку в этом случае меняются знаки проекций элементарной дуги на координатные оси:
Остальные свойства аналогичны свойствам криволинейного интеграла первого рода.

Вычисление криволинейного интеграла второго рода

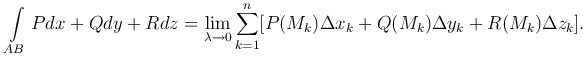
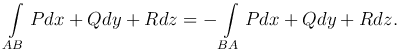
Если кривая L=AB задана параметрическими уравнениями

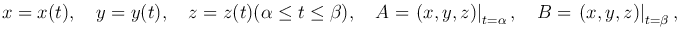
то

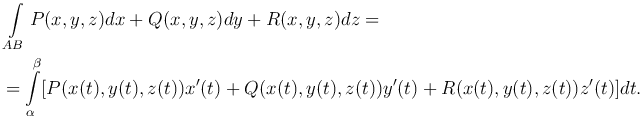
Если кривая L лежит в плоскости Oxy (z=0), то

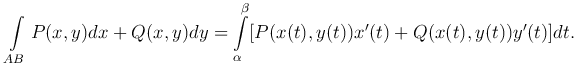
Если плоская кривая задана уравнением y=y(x), где a≤x≤b, y(x) - непрерывно дифференцируемая функция, то

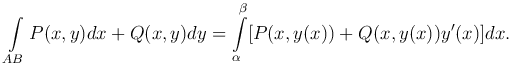
Связь между криволинейными интегралами первого и второго рода

Рассмотрим направленную дугу пространственной линии с началом в точке A и концом в точке B (рис. 2). Касательную в любой точке M дуги AB будем также считать направленной прямой. Углы, образуемые касательной с координатными осями Ox, Oy, Oz, обозначим соответственно через α, β, γ.

Рис. 2

Вектор dl=(dx,dy,dz), где dl - дифференциал длины дуги, направлен по касательной, поэтому

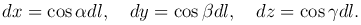
Следовательно,

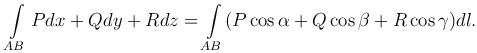
Эта формула выражает связь между криволинейными интегралами первого и второго рода. Если кривая AB лежит в плоскости Oxy (z=0), то

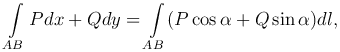
где α - угол между касательной и осью Ox.