Условия независимости криволинейного интеграла от пути интегрирования

Определение. Трехмерная область V называется поверхностно односвязной, если для любого замкнутого контура γ, принадлежащего этой области, найдется поверхность, целиком лежащая внутри V, имеющая данный контур своей границей.

Примеры поверхностно односвязной области: шар; область, ограниченная эллипсоидом; область, заключенная между двумя концентрическими сферами и т.п.

Пример поверхностно неодносвязной области: шар, из которого вырезан цилиндр.

Теорема. Если функции P=P(x,y,z), Q=Q(x,y,z), R=R(x,y,z) и их частные производные первого порядка непрерывны в некоторой замкнутой ограниченной поверхностно-односвязной области V, то следующие четыре утверждения равносильны.

1. Криволинейный интеграл по любому замкнутому контуру, лежащему внутри V, равен нулю:
2. Криволинейный интеграл не зависит от выбора пути, соединяющего точку A и точку B области V:
3. Выражение Pdx+Qdy+Rdz является полным дифференциалом, т.е.

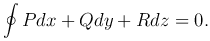
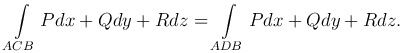
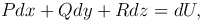
где U=U(x,y,z) - некоторая функция, определенная в области V.
4. Выполняются равенства:

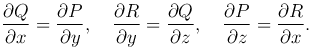
Замечание. Если криволинейный интеграл не зависит от пути интегрирования, то

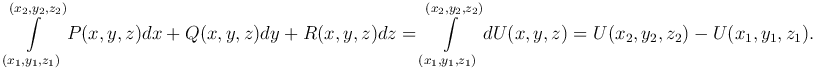
Следовательно, для вычисления криволинейного интеграла достаточно найти функцию U(x,y,z), определенную в предыдущей теореме п.3, и интеграл равен разности значений этой функции в конечной и начальной точке пути интегрирования.