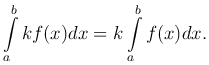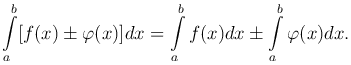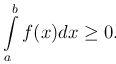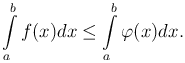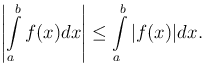Определенный интеграл

Прежде, чем дать определение определенного интеграла рассмотрим математические модели некоторых задач геометрии и механики с использованием определенного интеграла.

Задача о площади криволинейной трапеции

Рассмотрим криволинейную трапецию aABb, то есть плоскую фигуру, ограниченную сверху графиком функции y=f(x) (f(x) ≥ 0), слева и справа - отрезками aA и bB прямых x=a, x=b, снизу - осью Ox. Отрезок [a,b] точками a=x₀ < x₁ < x₂ < … < x_n-1 < x_n=b разобьем на n элементарных отрезков [a, x₁], [x₁, x₂], …, [x_n-1, b], длины которых обозначим через Δ x_k=x_k-x_k-1 (k=1, …, n). В каждом из элементарных отрезков [x_k-1, x_k] выберем произвольно точку ξ_k и вычислим в ней значение данной функции f(ξ_k). Произведение f(ξ_k)Δ x_k выражает площадь прямоугольника с основанием Δ x_k и высотой f(ξ_k). Составим сумму всех таких произведений

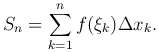
Эта сумма выражает площадь ступенчатой фигуры, состоящей из прямоугольников и приближенно заменяющей данную трапецию. Очевидно, что эта сумма, которая называется интегральной суммой для функции f(x) на отрезке [a, b], зависит от способа разбиения и выбора точек ξ_k.

Обозначим через λ длину наибольшего из элементарных отрезков [x_k-1, x_k] (k=1, …, n), то есть λ = max Δ x_k (k=1, …, n).

Число S называется пределом интегральной суммы S_n, если для любого числа ε > 0 можно указать такое число δ > 0, что при λ < δ выполняется неравенство |S_n-S| < ε независимо от выбора точек &xi_k на отрезках [x_k-1, x_k].

Предположим, что рассматриваемая сумма имеет предел, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю; этот предел и называется площадью криволинейной трапеции, то есть

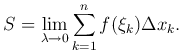
Задача о вычислении длины пути по заданной скорости

Пусть точка M движется прямолинейно с переменной скоростью ν = f(t). Вычислим длину пути, пройденного точкой M за промежуток времени от t₀ до T. Промежуток [t₀, T] разобьем на n элементарных промежутков [t₀, t₁], [t₁, t₂], …, [t_n-1, T] длиной Δ t_k = t_k-t_k-1 (t_n=T). В течение малого промежутка времени Δ t_k скорость движения можно приближенно считать постоянной и равной f(t'>sub>k), где t'_k - некоторое значение t из промежутка [t_k-1, t_k], поэтому длина пути, пройденного за этот промежуток, приближенно равна f(t'_k)Δ t_k. Складывая все частичные длины f(t'_k)Δ t_k, получаем приближенное значение длины пути, пройденного точкой за промежуток от t₀ до T:

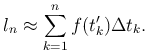
Перейдя к пределу, найдем точное значение длины пути:

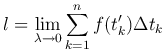
где λ = max Δ t_k (k = 1, …, n).

Итак, пройденный путь равен пределу интегральной суммы l_n функции ν = f(t) на отрезке [t₀, T].

Понятие определенного интеграла

Пусть дана функция y=f(x), определенная на отрезке [a, b], где a < b. Отрезок [a, b] точками a=x₀ < x₁ < x₂ < … < x_n-1 < x_n=b разобьем на n элементарных отрезков [a, x₁], [x₁, x₂], …, [x_k-1, x_k], …, [x_n-1, b], длины которых обозначим через Δ x_k, т.е. Δ x_k=x_k-x_k-1 (k = 1, …, n; x₀=a, x_n=b). В каждом из элементарных отрезков [x_k-1, x_k] выберем произвольную точку ξ_k, значение функции в этой точке f(ξ_k) умножим на длину отрезка Δ x_k, получим произведение f(ξ_k) Δ x_k. Составим сумму всех таких произведений

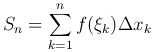
Эта сумма называется интегральной суммой для функции y=f(x) на отрезке [a, b].

Обозначим через λ длину наибольшего из элементарных отрезков [x_k-1, x_k] при данном n, т.е. λ = max Δ x_k (k = 1, …, n).

Определение. Определенным интегралом от функции y=f(x) на отрезке [a, b] называется конечный предел ее интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю.

Определенный интеграл обозначается символом 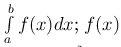называется подынтегральной функцией, x - переменной интегрирования, a - нижним пределом интегрирования, b - верхним пределом интегрирования.

Следовательно, по определению

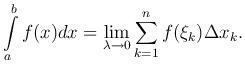
Функция, для которой существует этот предел, называется интегрируемой на отрезке [a, b].

Геометрический смысл определенного интеграла: определенный интеграл численно равен площади криволинейной трапеции, определяемой графиком функции y=f(x) на отрезке [a, b].

Справедливы следующие утверждения:

Если функция f(x) интегрируема на отрезке [a, b], то она и ограничена на этом отрезке.
Если функция f(x) интегрируема на отрезке [a, b], то она интегрируема на любом отрезке [c, d], содержащемся в [a, b].
Если функция f(x) непрерывна на отрезке [a, b], то она и интегрируема на этом отрезке.
Если функция f(x) имеет на отрезке [a, b] конечное число точек разрыва первого рода, то она интегрируема на [a, b].

Основные свойства определенного интеграла

Положим по определению, что
Если функция f(x) интегрируема на наибольшем из отрезков [a, b], [a, c], [c, b], то она интегрируема на двух других отрезках, причем

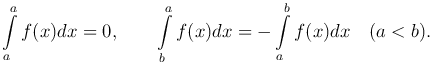
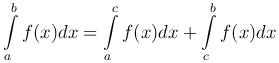
при любом расположении точек a, b, c.
Если функция f(x) интегрируема на отрезке [a, b], то функция kf(x), где k=const, также интегрируема на этом отрезке, причем
Если f(x) и φ(x) - функции, интегрируемые на отрезке [a, b], то их сумма и разность также интегрируемы на этом отрезке, причем
Если функция f(x) интегрируема на отрезке [a, b], где a < b, и f(x) ≥ 0 для всех x ∈ [a, b], то
Если функции f(x) и φ(x), интегрируемые на отрезке [a, b], где a < b, и f(x) ≤ φ(x) для всех x ∈ [a, b], то
Если функция f(x) интегрируема на отрезке [a, b], где a < b, то функция |f(x)| также интегрируема на [a, b], причем