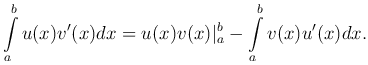Оценка определенного интеграла

Оценка определенного интеграла. Теорема о среднем

Теорема. Если функция f(x) интегрируема на отрезке [a, b], где a < b, и для всех x ∈ [a, b] выполняется неравенство

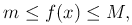
то

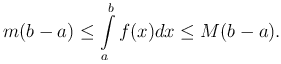
С помощью неравенств из теоремы можно оценить определенный интеграл, т.е. указать границы, между которыми заключено его значение. Эти неравенства выражают оценку определенного интеграла.

Теорема [Теорема о среднем]. Если функция f(x) интегрируема на отрезке [a, b] и для всех x ∈ [a, b] выполняются неравенства m ≤ f(x) ≤ M, то

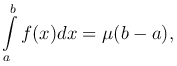
где m ≤ μ ≤ M.

Замечание. В случае, когда функция f(x) непрерывна на отрезке [a, b], равенство из теоремы принимает вид

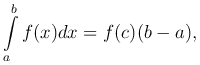
где c ∈ [a,b]. Число μ=f(c), определяемое данной формулой, называется средним значением функции f(x) на отрезке [a, b]. Это равенство имеет следующий геометрический смысл: площадь криволинейной трапеции, ограниченной непрерывной линией y=f(x) (f(x) ≤ 0), равна площади прямоугольника с тем же основанием и высотой, равной ординате некоторой точки этой линии.

Существование первообразной для непрерывной функции

Сначала введем понятие интеграла с переменным верхним пределом.

Пусть функция f(x) интегрируема на отрезке [a, b]. Тогда, каково бы ни было число x из [a, b], функция f(x) интегрируема на отрезке [a, b]. Поэтому на отрезке [a, b] определена функция

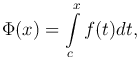
которую называют интегралом с переменным верхним пределом.

Теорема. Если подынтегральная функция непрерывна на отрезке [a, b], то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела, то есть

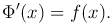
Следствие. Определенный интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции. Другими словами, для любой непрерывной на промежутке функции существует первообразная.

Замечание 1. Отметим, что если функция f(x) интегрируема на отрезке [a, b], то интеграл с переменным верхним пределом представляет собой непрерывную на этом отрезке функцию от верхнего предела. Действительно, из св.2 и теоремы о среднем имеем

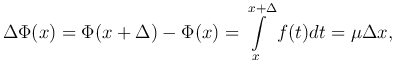
Замечание 2. Интеграл с переменным верхним пределом интегрирования используется при определении многих новых функций, например, 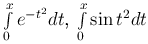. Эти функции не являются элементарными; как уже отмечалось, первообразные указанных подынтегральных функций не выражаются через элементарные функции.

Основные правила интегрирования

Формула Ньютона--Лейбница

Поскольку любые две первообразные функции f(x) отличаются на постоянную, то согласно предыдущей теореме можно утверждать, что любая первообразная Φ(x) непрерывной на сегменте [a, b] функции f(x) имеет вид

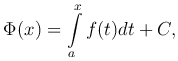
где C - некоторая постоянная.

Полагая в этой формуле x=a и x=b, используя св.1 определенных интегралов, найдем

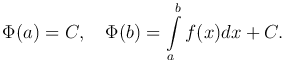
Из этих равенств вытекает соотношение

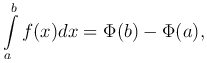которое называется формулой Ньютона-Лейбница.

Таким образом доказали следующую теорему:

Теорема. Определенный интеграл от непрерывной функции равен разности значений любой ее первообразной для верхнего и нижнего предела интегрирования.

Формулу Ньютона-Лейбница можно переписать в виде

где

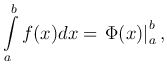
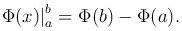
Замена переменной в определенном интеграле

Теорема. Если

функция f(x) непрерывна на отрезке [a, b];
отрезок [a, b] является множеством значений функции φ(t), определенной на отрезке α ≤ t ≤ β и имеющей на нем непрерывную производную;
φ(α)=a, φ(β)=b

то справедлива формула

Формула интегрирования по частям

Теорема. Если функции u=u(x), v=v(x) имеют непрерывные производные на отрезке [a, b], то справедлива формула