Двойной интеграл

Задачи, приводящие к двойным интегралам

Задача об объеме цилиндроида. Рассмотрим тело, ограниченное поверхностью z = f(x, y) с основанием S, лежащим в плоскости Oxy, и цилиндрической поверхностью с образующей параллельной оси Oz, и направляющей - линией, которая является границей области S (рис. 1 (а)). Такое тело называется цилиндроидом. Требуется вычислить объем этого цилиндроида.

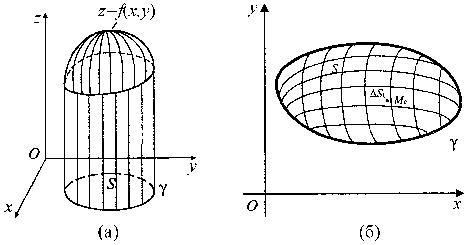
Рис. 1

Чтобы решить эту задачу, разобьем область S (рис. 1 (б)) сетью дуг на конечное число элементарных областей (ΔS₁), (ΔS₂), …, (ΔS_n), площади которых обозначим через ΔS₁, ΔS₂, …, ΔS_n соответственно. В каждой из элементарных областей (ΔS_k) (k=1, &hellip, n) выберем произвольно одну точку M_k(x_k,y_k) и значение функции в этой точке f(x_k,y_k) умножим на площадь области ΔS_k. Произведение f(x_k,y_k)ΔS_k равно объему цилиндрического тела с площадью основания ΔS_k и высотой h_k=f(x_k,y_k). Сумма всех таких произведений 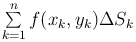выражает объем V_n ступенчатого цилиндрического тела, приближенно заменяющего цилиндроид, то есть

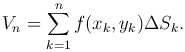
Обозначим диаметр элементарной области (ΔS_k) через d_k, а наибольший из диаметров - через λ_n, то есть 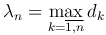. Очевидно, если λ_n→0, то n→∞.

Объемом цилиндроида называется предел объема соответствующего ступенчатого тела при λ_n→0:

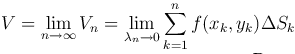
Задача о массе пластинки. Рассмотрим область S плоскости Oxy, ограниченную замкнутой линией в которой распределено вещество с плотностью p = f(x,y) ≥ 0. Такую область называют пластинкой. Требуется вычислить массу пластинки.

Область S сетью дуг разобьем на элементарные области (ΔS₁), (ΔS₂), …, (ΔS_n), площади которых обозначим через ΔS₁, ΔS₂, …, ΔS_n соответственно. Предположим, что в каждой элементарной области ΔS_k плотность постоянна и равна плотности в некоторой точке M_k(x_k,y_k) этой области, то есть p_k=f(x_k,y_k). Тогда произведение f(x_k,y_k)ΔS_k выражает приближенную массу элементарной пластинки (ΔS_k), а сумма всех таких произведений - приближенную массу m_n всей пластинки, то есть .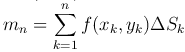

Точное значение массы всей пластинки получим перейдя к пределу при λ_n→0, где λ_n - наибольший из диаметров d_k области (ΔS_k): .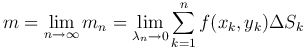

Таким образом, две различные задачи привели к рассмотрению предела одной и той же двумерной интегральной суммы. Это позволяет ввести общее понятие двойного интеграла.

Определение двойного интеграла

Рассмотрим функцию z = f(x,y), определенную в области S, ограниченной замкнутой линией. Область S разобьем сетью дуг на n элементарных областей (ΔS₁), (ΔS₂), …, (ΔS_n), имеющих площади ΔS₁, ΔS₂, …, ΔS_n соответственно. В каждой из элементарных областей (ΔS_k) (k = 1, … n) выберем произвольно одну точку M_k(x_k,y_k) и значение функции в этой точке f(x_k,y_k) умножим на площадь ΔS_k. Составим сумму всех таких произведений

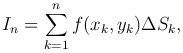
которая называется интегральной суммой для функции f(x,y) по области S.

Обозначим через d_k диаметр элементарной области (ΔS_k). Пусть λ_n - наибольший из всех диаметров, то есть .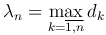

Определение. Число I называется пределом интегральной суммы I_n при λ_n→0, если для любого числа ε > 0 можно указать такое число δ > 0, что при λ_n < δ выполняется неравенство |I-I_n| < ε независимо от выбора точек M_k(x_k,y_k) в элементарных областях (ΔS_k).

Определение. Двойным интегралом от функции f(x,y) по области S называется предел ее интегральной суммы при λ_n→0:

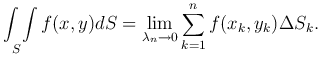
Функция f(x,y) называется подынтегральной функцией, а область S - областью интегрирования.

Двойной интеграл от функции f(x,y) по области S обозначается также следующим образом:

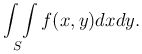
Утверждение. Предел 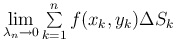существует, если функция z = f(x,y) непрерывна в замкнутой области, имеющей площадь.

Если существует данный предел, то функция f(x,y) называется интегрируемой в области S.

Таким образом, получили, что объем цилиндроида выражается следующим образом:

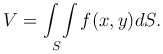
Геометрический смысл двойного интеграла: Двойной интеграл от функции f(x,y) по области S равен объему цилиндроида с основанием S и ограниченного сверху поверхностью z = f(x,y).

Также, масса пластинки выражается формулой:

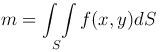
Физический смысл двойного интеграла: Если неотрицательная функция p = f(x,y) выражает поверхностную плотность пластинки S, то ее масса равна двойному интегралу от данной функции по данной области S.

Свойства двойного интеграла

1) Если функции f(x,y) и φ(x,y) интегрируемы в области S, то интегрируемы в ней и их сумма и разность, причем
2) Постоянный множитель можно выносить за знак двойного интеграла
3) Если f(x,y) интегрируема в области S, а эта область разбита на две непересекающиеся области S₁ и S₂ , то
4) Если f(x,y) и φ(x,y) интегрируемы в области S, в которой f(x,y) ≤ φ(x,y), то
5) Если f(x,y) интегрируема в области S, то |f(x,y)| также интегрируема в ней, причем
6) Если в области (S) функция f(x,y) удовлетворяет неравенствам m ≤ f(x,y) ≤ M, то

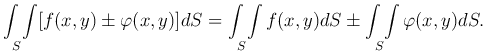
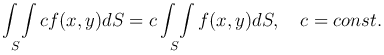
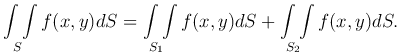
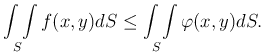
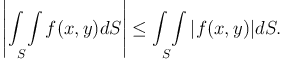
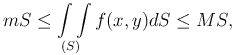
где S обозначает площадь области (S).

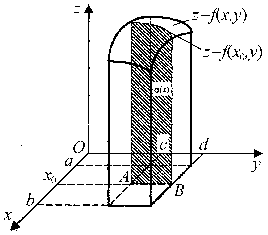
Вычисление двойного интеграла в прямоугольных декартовых координатах

Рис. 2

Случай прямоугольной области. Пусть требуется вычислить двойной интеграл

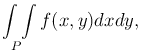
где область P является прямоугольником, определяемым неравенствами a ≤ x ≤ b, c ≤ y ≤ d (рис. 2). Предположим, что f(x,y) ≥ 0 и непрерывна в этом прямоугольнике, тогда данный двойной интеграл равен объему тела с основанием P, ограниченного сверху поверхностью z = f(x,y), с боков - плоскостями x = a, x = b, y = c, y = d:

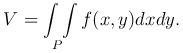
С другой стороны, объем тела 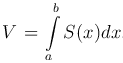, где S(x) - площадь сечения данного тела плоскостью, проходящей через точку x и перпендикулярной оси Ox.

Так как рассматриваемое сечение является криволинейной трапецией, ограниченной сверху графиком функции z = f(x,y), где x - фиксировано, c ≤ y ≤ d, то из геометрического смысла определенного интеграла имеем:

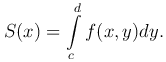
Отсюда имеем,

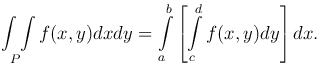
Здесь интеграл в правой части называется повторным интегралом.

Итак, вычисление данного двойного интеграла свелось к вычислению двух определенных интегралов; при вычислении "внутреннего" интеграла (в квадратных скобках) x считается постоянным.

Замечание. Эта формула верна для любой функции f(x,y).

Повторный интеграл обозначается так:

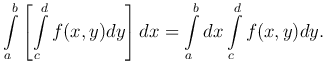
Аналогично можно показать, что

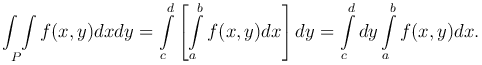
Таким образом,

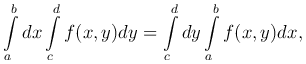
то есть результат интегрирования не зависит от порядка интегрирования.