Интегральное исчисление
Геометрические приложения определенного интеграла
Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x), слева и справа - прямыми x=a и x=b соответственно, снизу - осью Ox, вычисляется по формуле
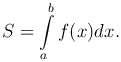
Площадь криволинейной трапеции, ограниченной справа графиком функции x=φ(y), сверху и снизу - прямыми y=d и y=c соответственно, слева - осью Oy:
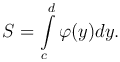
Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу - графиком функции y1=f1(x), слева и справа - прямыми x=a и x=b:
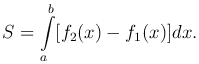
Площадь криволинейной фигуры, ограниченной слева и справа графиками функций x1=φ1(y) и x2=φ2(y), сверху и снизу - прямыми y=d и y=c соответственно:
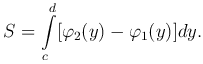
Рассмотрим случай, когда линия, ограничивающая криволинейную трапецию сверху, задана параметрическими уравнениями x = φ1(t), y = φ2(t), где α ≤ t ≤ β, φ1(α)=a, φ1(β)=b. Эти уравнения определяют некоторую функцию y=f(x) на отрезке [a, b]. Площадь криволинейной трапеции вычисляется по формуле
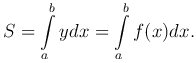
Перейдем к новой переменной x = φ1(t), тогда dx = φ'1(t) dt, а y=f(x)=f(φ1(t))=φ2(t), следовательно, \begin{displaymath}
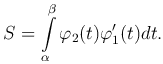
Рассмотрим криволинейный сектор OAB, ограниченный линией, заданной уравнением ρ=ρ(φ) в полярных координатах, двумя лучами OA и OB, для которых φ=α, φ=β.
Сектор разобьем на элементарные секторы OMk-1Mk (k=1, …, n, M0=A, Mn=B). Обозначим через
Δφk угол между лучами OMk-1 и OMk, образующими с полярной осью углы φk-1 и φk соответственно. Каждый из элементарных секторов OMk-1Mk заменим круговым сектором с радиусом ρk=ρ(φ'k),
где φ'k - значение угла φ из промежутка [φk-1, φk], и центральным углом
Δφk. Площадь последнего сектора выражается формулой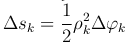 
.
Сумма
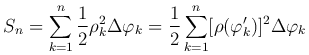
выражает площадь "ступенчатого" сектора, приближенно заменяющего данный сектор OAB.
Площадью сектора OAB называется предел площади "ступенчатого" сектора при n → ∞ и λ=max Δφk → 0:
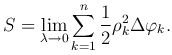
Так как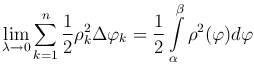 
, то
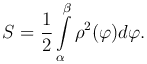
Пусть на отрезке [a, b] задана дифференцируемая функция y=f(x),
графиком которой является дуга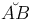 
. Отрезок [a,b] разобьем на n частей точками x1, x2, …, xn-1. Этим точкам будут соответствовать точки M1, M2, …, Mn-1 дуги , соединим их ломаной линией, которую называют ломаной, вписанной в дугу . Периметр данной ломаной
обозначим через sn, то есть
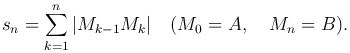
Определение. Длиной дуги линии называется предел периметра вписанной в нее ломаной, когда число звеньев Mk-1Mk неограничено возрастает, а длина наибольшего из них стремится к нулю:
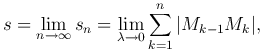
где λ - длина наибольшего звена.
Будем отсчитывать длину дуги от некоторой ее точки, например, A. Пусть в точке M(x,y) длина дуги 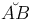равна s, а в точке M'(x+Δ x,y+Δy) длина дуги 
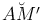равна s+Δs, где ,i>Δs - длина дуги 
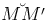. Из треугольника MNM' находим длину хорды : 
.
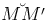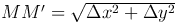Из геометрических соображений следует, что
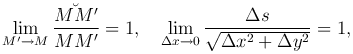
то есть бесконечно малая дуга линии и стягивающая ее хорда эквивалентны.
Преобразуем формулу, выражающую длину хорды :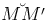
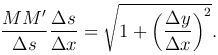
Переходя к пределу в этом равенстве, получим формулу для производной функции s=s(x):
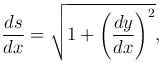
из которой находим
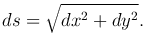
Эта формула выражает дифференциал дуги плоской кривой и имеет простой геометрический смысл: выражает теорему Пифагора для бесконечно малого треугольника MTN (ds=MT,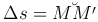 
).
Дифференциал дуги пространственной кривой определяется формулой
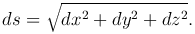
Рассмотрим дугу пространственной линии, заданной параметрическими уравнениями
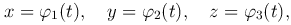
где α ≤ t ≤ β, φi(t) (i=1, 2, 3) - дифференцируемые функции аргумента t, то
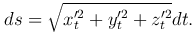
Интегрируя это равенство по промежутку [α, β], получаем формулу для вычисления длины этой дуги линии
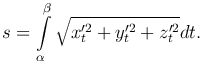
Если линия лежит в плоскости Oxy, то z=0 при всех t∈[α, β], поэтому
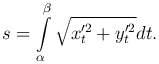
В случае, когда плоская линия задана уравнением y=f(x) (a≤x≤b), где f(x) - дифференцируемая функция, последняя формула принимает вид
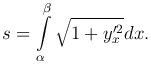
Пусть плоская линия задана уравнением ρ=ρ(φ) (α≤φ≤β) в полярных координатах. В этом случае имеем параметрические уравнения линии x=ρ(φ) cos φ, y=ρ(φ) sin φ, где в качестве параметра берется полярный угол φ. Поскольку
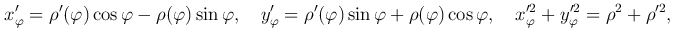
то формула, выражающая длину дуги линии ρ=ρ(φ) (α≤φ≤β) в полярных координатах, имеет вид
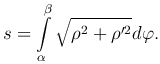
Найдем объем тела, если известна площадь любого поперечного сечения этого тела, перпендикулярного некоторому направлению.
Разобьем данное тело на элементарные слои плоскостями, перпендикулярными оси Ox и определяемыми уравнениями x=const. Для любого фиксированного x∈[a,b] известна площадь S=S(x) поперечного сечения данного тела.
Элементарный слой, отсеченный плоскостями x=xk-1, x=xk (k=1, …, n, x0=a, xn=b), заменим цилиндром с высотой Δxk=xk-xk-1 и площадью основания S(ξk), ξk∈[xk-1,xk].
Объем указанного элементарного цилиндра выражается формулой Δvk=E(ξk)Δxk. Составим сумму всех таких произведений
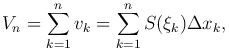
являющуюся интегральной суммой для данной функции S=S(x) на отрезке [a, b]. Она выражает объем ступенчатого тела, состоящего из элементарных цилиндров и приближенно заменяющего данное тело.
Объемом данного тела называют предел объема указанного ступенчатого тела при λ→0, где λ - длина наибольшего из элементарных отрезков Δxk. Обозначим через V объем данного тела, тогда по определению
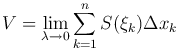
С другой стороны,
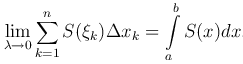
Следовательно, объем тела по заданным поперечным сечениям вычисляется по формуле
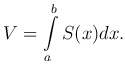
Если тело образовано вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху дугой непрерывной линии y=f(x), где a≤x≤b, то S(x)=πf2(x) и последняя формула принимает вид:
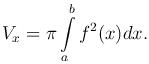
Замечание. Объем тела, полученного вращением криволинейной трапеции, ограниченной справа графиком функции x=φ(y) (c ≤ x ≤ d), вокруг оси Oy вычисляется по формуле
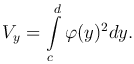
Рассмотрим поверхность, полученную вращением дуги линии y=f(x) (a≤x≤b) вокруг оси Ox (предположим, что функция y=f(x) имеет непрерывную производную). Фиксируем значение x∈[a,b], аргументу функции придадим приращение dx, которому соответствует "элементарное кольцо", полученное вращением элементарной дуги Δl. Это "кольцо" заменим цилиндрическим кольцом - боковой поверхностью тела, образованного вращением прямоугольника с основанием, равным дифференциалу дуги dl, и высотой h=f(x). Разрезав последнее кольцо и развернув его, получим полоску шириной dl и длиной 2πy, где y=f(x).
Следовательно, дифференциал площади поверхности выразится формулой
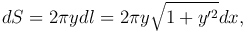
откуда
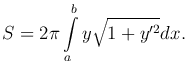
Эта формула выражает площадь поверхности, полученной вращением дуги линии y=f(x) (a≤x≤b) вокруг оси Ox.