Формула Грина

Формула Грина устанавливает связь между двойным интегралом по области S и криволинейным интегралом по контуру Γ, ограничивающему эту область (рис. 3). Будем считать, что область S является стандартной в направлении каждой координатной оси и снизу ограничена графиком функции y=y₁(x) (дугой ACB), сверху - графиком функции y=y₂(x) (дугой ADB), которые вместе составляют замкнутый контур Γ.

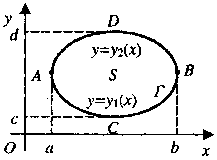
Рис. 3

Пусть в области S и на ее границе Γ заданы функции P(x,y), Q(x,y), непрерывными вместе со своими частными производными P'_y(x,y), Q'_x(x,y), тогда

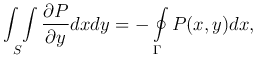
где обход контура Γ совершается в положительном направлении, т.е. против часовой стрелки (область S остается слева).

Аналогично получаем

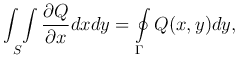
где обход контура Γ также совершается в положительном направлении. Вычитая одну формулу из другой, получим

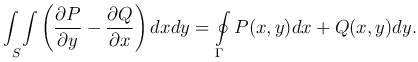
Это формула Грина.

Замечание 1. Если обход конура Γ совершается в отрицательном направлении, т.е. по часовой стрелке (область S остается справа), то формула Грина примет вид

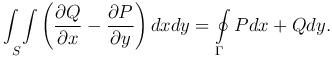
Замечание 2. Формула Грина дает возможность вычислять площадь области с помощью криволинейного интеграла: если P(x,y)=-y, Q(x,y)=x, то

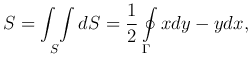
где обход контура Γ совершается против часовой стрелки.