Несобственные интегралы

При введении понятия определенного интеграла предполагалось, что выполняются условия:

1) пределы интегрирования a и b являются конечными;
2) подынтегральная функция f(x) ограничена на отрезке [a, b].

В этом случае определенный интеграл называют собственным. Если хотя бы одно из этих двух условий не выполняется, то интеграл называется несобственным.

Интегралы с бесконечными пределами

Пусть функция y=f(x) непрерывна при любом x ≥ a. Рассмотрим интеграл с переменным верхним пределом

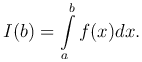
Предположим, что при b → +∞ этот интеграл, который является дифференцируемой функцией верхнего предела, имеет конечный предел. Этот предел называется сходящимся несобственным интегралом от функции f(x) по промежутку [a, +∞) и обозначается

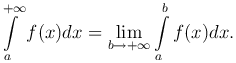
Если этот предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.

Геометрически несобственный интеграл от неотрицательной функции выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции y=f(x), слева - отрезком прямой x=a, снизу - осью Ox. В случае сходящегося интеграла эта площадь является конечной, в случае расходящегося - бесконечной.

Если F(x) - первообразная для функции f(x), то

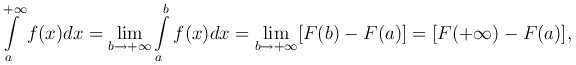
где .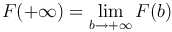

Аналогично определяется несобственный интеграл с бесконечным нижним пределом

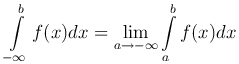
и несобственный интеграл с обоими бесконечными пределами

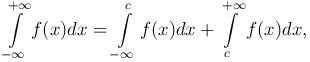
где c - любая точка из интервала (-∞,+∞).

Теорема [Теорема сравнения]. Если при x ≥ a выполнены неравенства 0 ≤ φ(x) ≤ f(x) и 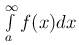сходится, то сходится и 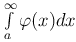, причем 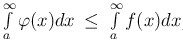; если 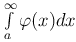расходится, то расходится и интеграл .

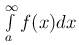Определение. Пусть функция f(x) интегрируема в обычном смысле на каждом конечном отрезке a ≤ x ≤ B, a < B < +∞. Несобственный интеграл 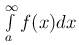называется абсолютно сходящимся, если сходится интеграл .

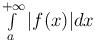Теорема. Если в промежутке [a, +∞) функция f(x) меняет знак и 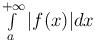сходится, то сходится также .

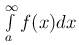Другими словами, если интеграл 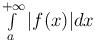сходится абсолютно, то он сходится.

Замечание. Из сходимости интеграла 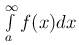не следует его абсолютная сходимость. Например, интеграл 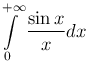сходится, а интеграл 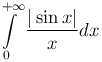расходится.

Определение. Интеграл

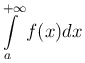
называется условно сходящимся, если он сходится, в то время как интеграл

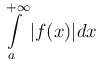
расходится.

Интегралы от неограниченных функций

Если функция y=f(x) не ограничена в окрестности точки c, которая называется особой точкой, отрезка [a, b] и непрерывна при a ≤ x < c и c < x ≤ b, то несобственный интеграл от этой функции определяется формулой

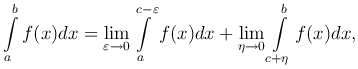
где ε > 0, η > 0. Этот несобственный интеграл называется сходящимся, если существуют и конечны оба предела в правой части.

В случае c = b или c = a получаем

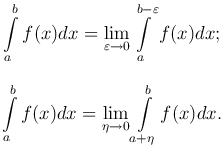
Эти несобственные интегралы называются сходящимися, если существует конечный предел соответствующего определенного интеграла; в противном случае интеграл называется расходящимся.

Абсолютная и условная сходимость определяются, как и в случае интегралов с бесконечными пределами интегрирования. Из абсолютной сходимости следует также сходимость интеграла и верна следующая теорема сравнения:

Теорема [Теорема сравнения]. Если b - единственная особая точка f(x) на [a, b] и |f(x)| ≤ g(x) при все x ∈ [a, b), достаточно близких к b, то из сходимости интеграла 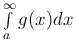следует абсолютная сходимость интеграла .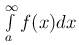