Неопределенный интеграл

Рассмотрим физическую задачу. Пусть для любого момента времени x задана мгновенная скорость f(x) движущейся по оси Oy материальной точки и известно положение y₀ этой точки в начальный момент времени x=x₀. Требуется найти закон движения этой точки.

Поскольку мгновенная скорость f(x) является производной функции y=F(x), определяющей закон движения материальной точки по оси Oy, то задача сводится к отысканию по данной функции f(x) такой функции F(x), производная F'(x) которой равна f(x). Математически эта функция F(x) называется первообразной функции f(x)$.

Очевидно, что если функция F(x) является первообразной функции f(x), то и функция F(x)+C, где C - любая постоянная, также является первообразной функции f(x). Совокупность всех первообразных одной и той же функции f(x) называется определенным интегралом от функции f(x) и обозначается символом ∫ f(x) dx. Таким образом,

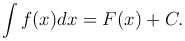
Интересующий нас закон движения точки, имеющей мгновенную скорость f(x), определяется функцией y=F(x)+C, где F(x) - некоторая первообразная функции f(x), а C - некоторая постоянная. Для определения постоянной воспользуемся тем, что y=y₀ в начальный момент времени x=x₀, т.е. y₀=F(x₀)+C, откуда C=y₀-F(x0). Таким образом, интересующий нас закон движения имеет вид

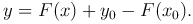
Решение свелось к нахождению первообразной функции.

Понятие первообразной функции

Определение. Функция F(x) называется первообразной функцией (или просто первообразной) для функции f(x) на интервале (a, b), если в любой точке x интервала (a, b) функция F(x) дифференцируема и имеет производную F'(x) равную f(x).

Аналогично определяется первообразная для функции f(x) на отрезке, на бесконечной прямой, на полупрямой.

Пример. Функция 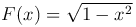является первообразной для функции 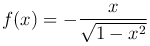на интервале (-1,1).

Пример. Функция F(x)=sin x является первообразной для функции f(x)=cos x на бесконечной прямой (-∞, +∞).

Если F(x) является первообразной для функции f(x) на интервале (a,b), то и функция F(x)+C, где C - любая постоянная, является первообразной для функции f(x) на интервале (a,b).

Теорема [Основная теорема]. Если F₁(x) и F₂(x) - любые первообразные для функции f(x) на интервале (a,b), то всюду на этом интервале F₁(x)-F₂(x)=C, где C - некоторая постоянная.

Другими словами, две любые первообразные для одной и той же функции могут отличаться только на постоянную.

Следствие. Если F(x) - одна из первообразных функций для функции f(x) на интервале (a,b), то любая первообразная Ψ(x) для функции f(x) на интервале (a,b) имеет вид Ψ(x)=F(x)+C, где C - некоторая постоянная.

Понятие неопределенного интеграла

Определение. Совокупность всех первообразных функций для данной функции f(x) на интервале (a,b) называется неопределенным интегралом от функции f(x) и обозначается символом

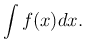
Знак ∫ называется знаком интеграла, выражение f(x)dx - подынтегральным выражением, а сама функция f(x) - подынтегральной функцией.

Если F(x) - одна из первообразных функций для функции f(x) на интервале (a,b), то по следствию из предыдущей теоремы

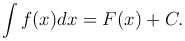
где C - любая постоянная.

Операция нахождения первообразной данной функции называется интегрированием.

Пример. 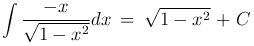на интервале (-1,1), так как функция 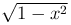является одной из первообразных для функции 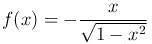на этом интервале.

Пример. ∫ cos x dx = sin x + C на (-∞, +∞), так как функция F(x)=sin x является одной из первообразных для функции f(x)=cos x на бесконечной прямой.

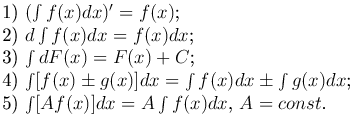
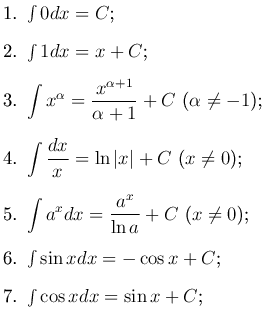
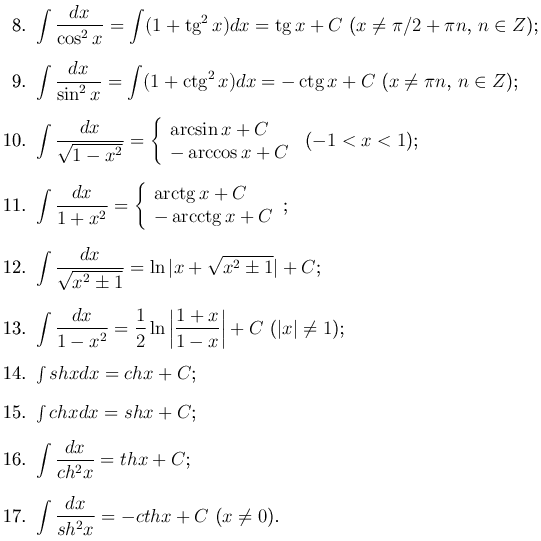
Основные свойства неопределенного интеграла

Таблица основных неопределенных интегралов

Замечание. При операции дифференцирования элементарной функции всегда получаем элементарную функцию. С операцией интегрирования дело обстоит иначе. Интегралы от некоторых элементарных функций не являются элементарными функциями. Например,

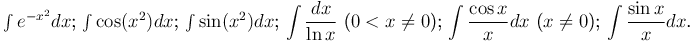
Каждый из этих интегралов представляет собой функцию не являющуюся элементарной.