Интегрирование иррациональных и тригонометрических функций

Интегрирование простейших иррациональных функций

В некоторых случаях интегралы от иррациональных функций удается рационализировать, т.е. с помощью подходящей подстановки свести к интегралам от рациональных дробей. Рассмотрим некоторые типичные случаи.

1. Если корни в подынтегральном выражении имеют вид:

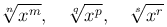
и т.д., то оно преобразуется в рациональную дробь с помощью подстановки x=t^k, где k - наименьшее общее кратное показателей корней, т.е. чисел n, q, s, ….

Если выражение под знаком интеграла содержит только корни

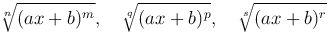
и т.д., то оно приводится к рациональной дроби с помощью подстановки ax+b=t^k, где k - наименьшее общее кратное показателей корней, т.е. чисел n, q, s, …

3. Если выражение под знаком интеграла содержит только корни

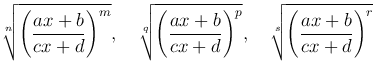
и т.д., то оно приводится к рациональной дроби с помощью подстановки 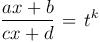, где k - наименьшее общее кратное показателей корней, т.е. чисел n, q, s, …

4. Если подынтегральное выражение представляет собой дифференциальный бином, т.е. равно x^m(a+bxⁿ)^p dx, где m, n, p - рациональные числа, то данный интеграл сводится к интегралу от рациональной дроби в следующих трех случаях:

а) p - целое число; тогда применяется подстановка x=t^k, где k - общий знаменатель дробей m и n;

б) 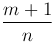- целое число; тогда используется подстановка a+bxⁿ=t^k, где k - знаменатель числа p;

в) 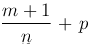-- целое число; в этом случае делается подстановка ax^-n+b=t^k, где k - знаменатель числа p.

Неопределенный интеграл выделением полного квадрата в подкоренном выражении и введением новой переменной u=x+b, в зависимости от знака A, приводится к одному из интегралов:

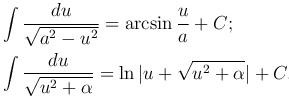
Неопределенный интеграл , в зависимости от знака A, приводится к одному из интегралов:

Интегрирование некоторых тригонометрических выражений

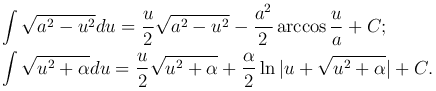
Неопределенные интегралы вида

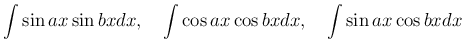
с помощью тригонометрических формул

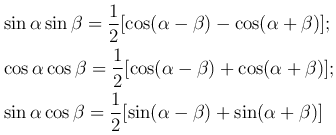
приводятся к интегралам

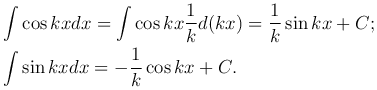
Неопределенные интегралы вида 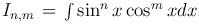, где n и m - натуральные числа, находятся с помощью тригонометрических формул

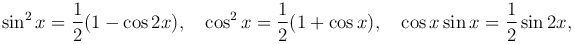
если n и m являются четными. Если хотя бы одно из чисел n и m - нечетное, то от нечетной степени отделяется множитель и вводится новая переменная. В частности, если m=2k+1, то

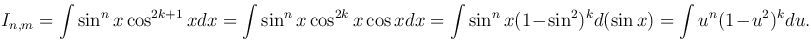
Этот интеграл находится непосредственно, как интеграл от алгебраического многочлена.

Рассмотрим неопределенный интеграл

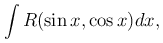
где R(sin x, cos x) - рациональная функция от sin x и cos x.

Введем новую переменную по формуле , тогда

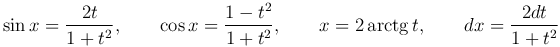
В результате указанной замены переменной получаем

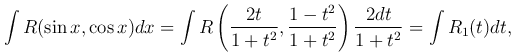
где R₁(t) - рациональная функция переменной t.