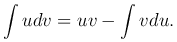Основные методы интегрирования

Рассмотрим основные методы вычисления неопределенных интегралов.

Непосредственное интегрирование

Этот метод основан на использовании основных свойств неопределенного интеграла и таблицы интегралов.

Интегрирование заменой переменной (подстановкой)

Теорема. Если F(x) - первообразная функции f(x), а x=φ(t) - дифференцируемая функция, то функция 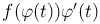также имеет первообразную, причем

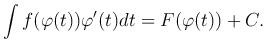
Пусть нам требуется вычислить интеграл

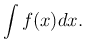
В ряде случаев удается выбрать в качестве новой переменной такую дифференцируемую функцию t=φ(x), что имеет место равенство

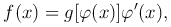
причем функция g(t) легко интегрируется, то есть интеграл

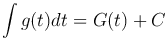
просто вычисляется. Теорема позволяет написать следующую формулу для нашего интеграла:

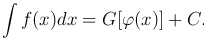
Этот прием вычисления интеграла ∫ f(x) dx и называется интегрированием путем замены переменной.

Конечно, такой прием применим не ко всякому интегралу. Кроме того, выбор правильной подстановки в значительной мере определяется искусством вычислителя. Однако можно следовать двум полезным подсказкам:

Если под знаком интеграла стоит сложная функция f(φ(x)), то, как правило, используется подстановка t=φ(x).
Если в подынтегральном выражении есть готовый дифференциал функции φ(x), т.е. выражение φ'(x)dx, то имеет смысл попробовать подстановку t=φ(x). Поэтому полезно помнить следующие формулы для наиболее часто встречающихся дифференциалов:

Интегрирование по частям

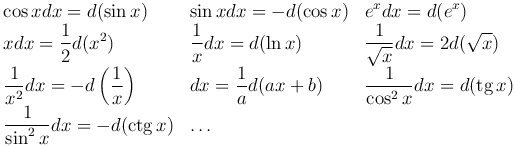
Теорема. Пусть производные функции u(x) и v(x) существуют и непрерывны на заданном интервале. Тогда имеет место равенство

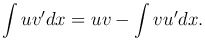
Эта формула называется формулой интегрирования по частям.

Так как v'(x)dx=dv(x), u'(x)dx=du(x), то можно последнюю формулу записать в более компактном виде