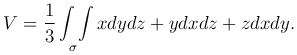Интегральное исчисление
Формула Остроградского
Формула Остроградского выражает связь между тройным интегралом по пространственной области и интегралом по поверхности, ограничивающей эту область.
Рассмотрим стандартную пространственную область V, ограниченную сверху поверхностью z=z2(x,y), снизу - поверхностью z=z1(x,y), а также боковой цилиндрической поверхностью с образующей параллельной оси Oz (рис. 3). Эта пространственная область, спроектированная на плоскость Oxy даст область S.
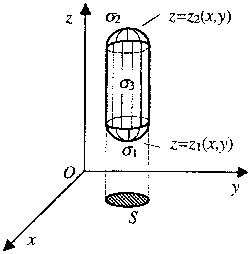
Рис. 3
Пусть функции R(x,y,z) и R'z(x,y,z) определены и непрерывны в области V и на ее границе. Т.к.
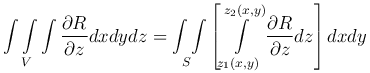
и
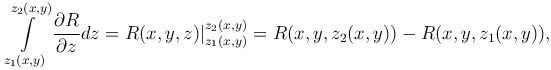
то
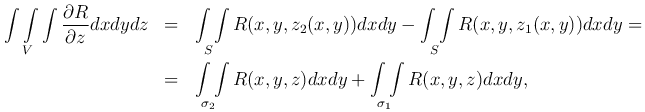
где первый интеграл берется по верхней стороне поверхности σ2, а второй интеграл - по нижней стороне поверхности σ1.
Прибавив еще один интеграл по цилиндрической поверхности σ3, ограничивающей область V:
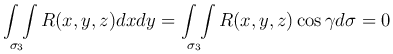
(т.к. на σ3 вектор нормали n перпендикулярен оси Oz, то cos γ=0), получим
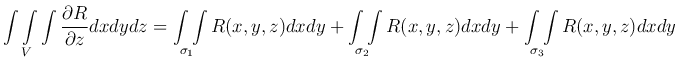
или
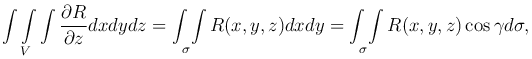
где σ=σ1+σ2+σ3 - поверхность, ограничивающая объем V; интеграл берется по внешней стороне поверхности.
При соответствующих предположениях относительно области V и функцией Q(x,y,z), Q'y(x,y,z), P(x,y,z), P'x(x,y,z) аналогично находим
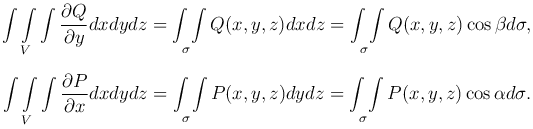
Складывая эти три равенства, получим формулу Остроградского
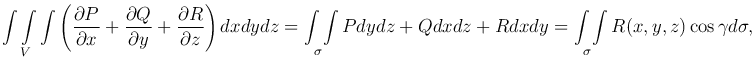
или
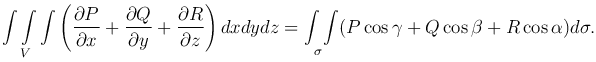
Замечание. С помощью формулы Остроградского можно найти выражение объема через интеграл по поверхности, ограничивающей
этот объем. Действительно,подберем функции $P$, $Q$, $R$ так, чтобы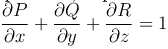 
, тогда
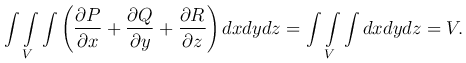
Пусть, например, P=x/3, Q=y/3, R=z/3, тогда
