Интегральное исчисление

Приведем способы вычисления неопределенных интегралов для рациональных дробей.

Интегрирование рациональных дробей с квадратным трехчленом в знаменателе

Пусть требуется найти ∫ R(x) dx, где

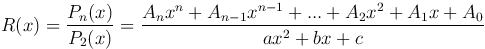
Произведя деление получим

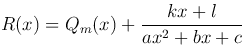
где Q_m(x) - многочлен, степень которой ниже степени многочлена P_n(x):

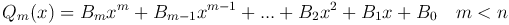
Первообразная от многочлена Q_m(x) находится легко:

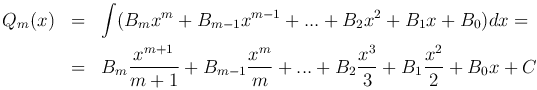
Остается найти первообразную функции

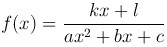
Посмотрим сначала как интегрируются простейшие дроби:

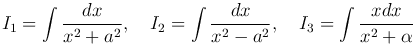
Первый интеграл приводится к табличному преобразованием подынтегрального выражения:

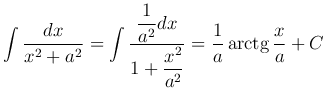
Чтобы найти второй интеграл, преобразуем подынтегральную функцию

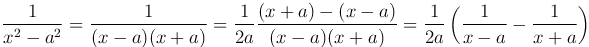
Следовательно,

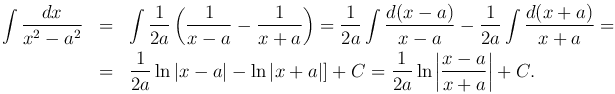
Третий интеграл также легко приводится к табличному

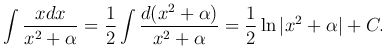
Неопределенный интеграл

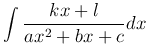
в случае k=0 приводится к интегралу I₁ или I₂; в случае k ≠ 0 - к интегралу I₃ и одному из интегралов I₁, I₁. Основной способ нахождения этого интеграла состоит в предварительном выделении полного квадрата из квадратного трехчлена и вычислении простейших дробей.

Интегрирование рациональных функций

Интегрирование рациональных дробей означает нахождение неопределенных интегралов ∫ R(x) dx, где R(x) - правильная рациональная дробь, т.е.

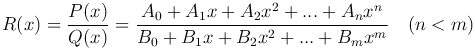
Нахождение указанных интегралов основано на разложении рациональной дроби в сумму элементарных дробей, т.е. дробей вида

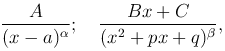
где α, β - натуральные числа; a, p, q, A, B, C - действительные числа; p²-4q < 0 (дискриминант отрицательный).

Теорема. Если дана рациональная дробь R(x) и

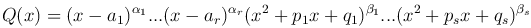
где a_i (i=1,2,…,r) - попарно различные вещественные корни многочлена Q(x) кратности α_i, а x²+p_kx+q_k - квадратный трехчлен кратности &beta_k, дискриминант которого отрицателен, то существуют вещественные числа

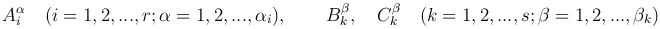
такие, что

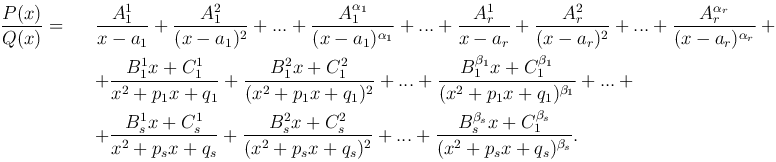
Отметим, что каждому действительному корню a кратности α многочлена Q(x) в этом разложении соответствует сумма α элементарных дробей:

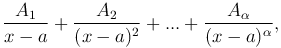
а каждому квадратному трехчлену x²+p x+q_k кратности β - сумма