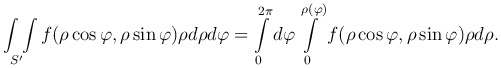Интегральное исчисление
Случай стандартной области
Определение. Стандартной областью в направлении данной оси называется такая область, для которой любая прямая, параллельная этой оси и имеющая с данной областью общие точки, пересекает границу области только в двух точках: M - точка "входа", N - точка "выхода".
Предположим, что ограниченная область S является стандартной в направлении оси Oy и ограничена сверху графиком функции y2 =y2(x), снизу - графиком функции y1 =y1(x), слева - отрезком прямой x = a, справа - отрезком прямой x = b (рис. 1).
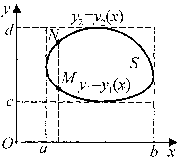
Рис. 1
Замечание. В некоторых случаях отрезки прямых x = a и x = b могут вырождаться в точку.
Пусть P = {a ≤ x ≤ b, c ≤ y ≤ d} - минимальный прямоугольник, в котором заключена данная область S. Пусть в области S определена и непрерывна функция z = f(x,y). Введем новую функцию:
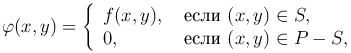
тогда по свойству 3 двойного интеграла
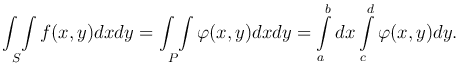
Так как отрезок [y1(x), y2(x)] ∈ S, то φ(x,y) =f(x,y) при y1(x) ≤ y ≤ y2(x), φ(x,y) = 0, если y лежит вне этого отрезка, то при фиксированном x
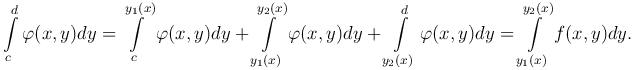
Следовательно,
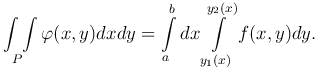
Таким образом, получаем окончательную формулу:
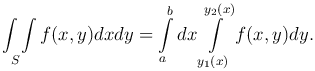
Если область S является стандартной в направлении оси Ox и ограничена слева кривой x = x1(y), справа - кривой x = x2(y), снизу - отрезком прямой y = c, сверху - отрезком прямой y = d, то аналогично можно доказать, что
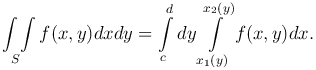
Замечание. Если область S является стандартной в направлении осей Ox и Oy, то будут выполнены оба равенства, поэтому
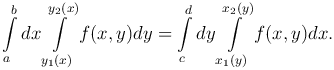
По этой формуле осуществляется изменение порядка интегрирования при вычислении соответствующего двойного интеграла.
Если область интегрирования S не принадлежит ни к одному рассмотренному виду, то ее разбивают на части, каждая из которых является стандартной областью. Тогда двойной интеграл по всей области в соответствии с пятым свойством двойного интеграла равен сумме двойных интегралов по каждой части области.
Замена переменных в двойном интеграле связана с введением криволинейных координат на плоскости.
В плоскости Oxy рассмотрим область S, ограниченную гладкой линией γ (рис. 2). Пусть
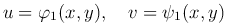(1
)
- однозначные функции переменных x и y, непрерывные в области S и имеющие в ней непрерывные частные производные.
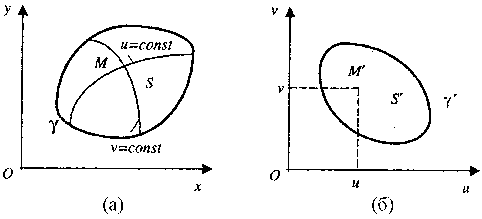
Рис. 2
Предположим, что эти уравнения однозначно разрешимы относительно x и y, то есть
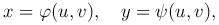(2)
где φ(u,v), ψ(u,v) - непрерывные функции в некоторой области S' плоскости Ouv и имеющие в ней непрерывные частные производные.
Каждой точке M(x,y) ∈ S формулы (1)) ставят в соответствие единственную точку M'(u,v) ∈ S'. Обратно, любую точку M'(u,v) ∈ S' формулы (2) ставят в соответствие единственную точку M(x,y) ∈ S. Числа (u,v) называют при этом криволинейными координатами точки M.
Таким образом, формулы (1) устанавливают взаимно однозначное соответствие между точками S и S'. Другими словами, отображают область S на область S'.
Фиксируем значение u = u0, тогда прямой u = u0 в плоскости Ouv будет соответствовать в плоскости Oxy некоторая линия, параметрические уравнения которой
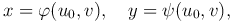
где v - параметр. Фиксируем значение v = v0, тогда прямой v = v0 в плоскости Ouv будет соответствовать в плоскости Oxy некоторая линия, параметрические уравнения которой
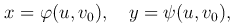
где u - параметр. Придавая поочередно u и v различные (возможные для них) значения, получаем два семейства линий на плоскости. Эти линии называются координатными.
Примером криволинейных координат являются полярные координаты, в этом случае u = ρ, v = φ; координатные линии - концентрические окружности и полупрямые, исходящие из начала координат. Прямоугольные координаты - частный случай криволинейных: u = x, v = y, координатные линии - прямые, параллельные осям координат.
Прямоугольнику N0 N1 N2 N3 (рис. 3(а)) в плоскости Ouv, ограниченному прямыми u = u0, u = u0 + Δu, v = v0, v = v0 + Δv, в плоскости Oxy соответствует криволинейный четырехугольник M0 M1 M2 M3, причем M0(x0, y0), M1(x1, y1), M2(x2, y2), M3(x3, y3) (рис. 3(б)), где x0 = φ(u0, v0), y0 = ψ(u0, v0), x1 = φ(u0+Δu, v0), y1 = ψ(u0 + Δv0), x2 = φ(u0 + Δu, v0 + Δv), y2 = ψ(u0 +Δu, v0 + Δv), x3 = φ(u0, v0 + Δv), y3 = ψ(u0, v0 +Δv).
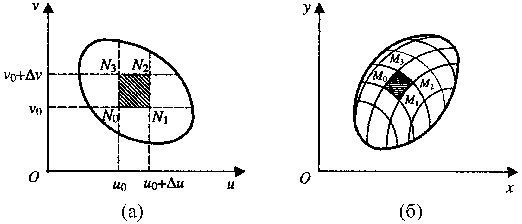
Рис. 3
С точностью до бесконечно малых высшего порядка площадь M0 M1 M2 M3 равна площади параллелограмма, построенного на векторах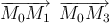 
. Площадь этого параллелограмма выражается формулой
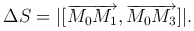
Координаты
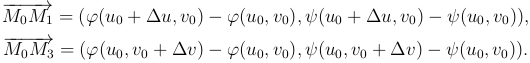
Применяя теорему Лагранжа, получаем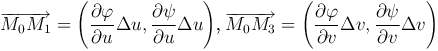 
. Следовательно,
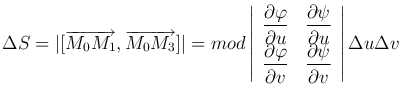
или ΔS = |J| ΔS', ΔS' = Δu Δv, где
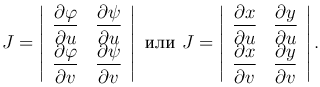
Определитель J называется функциональным определителем функций (2) или якобианом преобразования (2).
Предполагаем, что J ≠ 0.
Рассмотрим вопрос о замене переменных в двойном интеграле
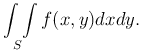
Предположим, что функция z = f(x, y) непрерывна в области S. Пусть в этой области заданы функции
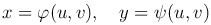
- непрерывные вместе со своими частными производными, тогда
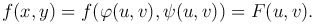
Составим интегральную сумму для этой функции:
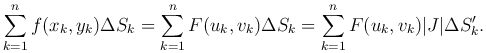
Переходя к пределу, получим искомую формулу:
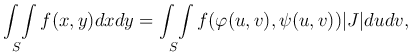
по которой осуществляется замена переменных в двойном интеграле.
Считая u = ρ, v = φ, находим якобиан данного преобразования:
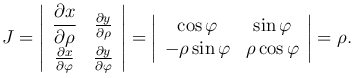
Тогда
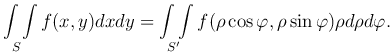
Если область S' ограничена лучами, образующими с полярной осью углы φ1 = α, φ2 = β, и кривыми ρ = ρ1(φ), ρ = ρ2(φ) (ρ1(φ) < ρ2(φ)), то
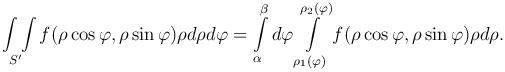
Если область S' охватывает начало координат, то
