Интегралы по поверхности

Поверхностный интеграл первого рода

Пусть на поверхности σ задана функция u=f(x,y,z) (рис. 1). Разобьем поверхность $\sigma$ сетью дуг линий на элементарные поверхности (Δσ_k), k=1,…,n, площадь которых обозначим через Δσ_k, k=1,…,n. На каждой элементарной поверхности (Δ&sigma_k) произвольным образом выберем точку M_k(x_k,y_k,z_k), значение функции в этой точке f(M_k)=f(x_k,y_k,z_k) умножим на площадь Δ&sigma_k и составим сумму всех таких произведений

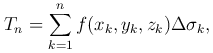
которая называется интегральной суммой функции u=f(x,y,z) по поверхности σ.

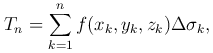
Рис. 1

Обозначим через d_k диаметр элементарной поверхности (Δσ_k), .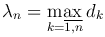

Определение. Если предел интегральной суммы T_n при λ_n→0 существует, то он и называется поверхностным интегралом первого рода.

По определению

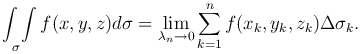
Определение. Поверхность называется гладкой, если она имеет в каждой своей точке касательную плоскость, положение которой меняется непрерывно при переходе от точки к точке.

Утверждение. Предел интегральной суммы T_n существует, если функция f(x,y,z) непрерывна, а поверхность σ является гладкой.

Свойства поверхностных интегралов первого рода аналогичны свойствам криволинейных интегралов первого рода.

Двусторонняя поверхность

На поверхности σ фиксируем точку M₀ и одно из направлений нормали к ней в этой точке, указав единичный вектор n, отложенный из точки M₀. Проведем из точки M₀ замкнутую линию Γ, целиком лежащую на поверхности σ и не имеющую общих точек с границей σ. Будем совершать обход линии Γ так, чтобы нормаль изменялась непрерывно, при этом вектор n в каждой точке M будет иметь вполне определенное направление (вообще говоря, отличное от направления в точке M₀). После возвращения обхода может оказаться:

1) вектор n принял первоначальное направление;
2) вектор n изменил направление на противоположное.

Определение. Поверхность σ называется двусторонней, если обход по любой замкнутой линии, лежащей на этой поверхности и не имеющей общих точек с ее границей, не меняет направления нормали к поверхности.

Двусторонней поверхностью является всякая гладкая поверхность, определяемая уравнением z=f(x,y) (рис. 2(а)). Действительно, выбрав направление нормального вектора n₁ к ней так, чтобы он составил с осью Oz острый угол, получим одну сторону поверхности (верхнюю). Выбрав это направление так, чтобы вектор n₂ составил с осью Oz тупой угол, получим другую сторону поверхности (нижнюю).

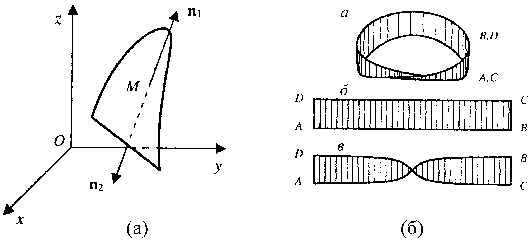
Рис. 2

Примеры двусторонней поверхности: плоскость и любая ее часть (круг, эллипс и т.д.); любая замкнутая поверхность, не имеющая точек самопересечения (сфера, эллипсоид и т.п.)

Двусторонняя поверхность называется также ориентируемой, а выбор ее определенной стороны - ориентацией поверхности.

Определение. Если на поверхности существует замкнутая линия, обход по которой меняет направление нормали, то поверхность называется односторонней.

Пример односторонней поверхности: лист Мёбиуса (рис. 2(б)). При обходе его средней линии направление нормали к нему меняется на противоположное.

Поверхностный интеграл второго рода

Рассмотрим функцию R=R(x,y,z), определенную и непрерывную на гладкой ориентируемой поверхности σ. Поверхность σ разобьем на n элементарных частей (Δσ_k), k=1,…,n. Выберем в каждой элементарной части точку M_k(x_k,y_k,z_k) и составим интегральную сумму:

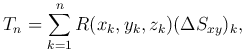
где (ΔS_xy)_k - величина проекции (Δ&sigma_k) на плоскость Oxy; она равна площади области, в которую проектируется (Δσ_k) на Oxy, взятой со знаком "плюс", если нормаль к поверхности в точке M_k образует с осью Oz острый угол, и со знаком "минус", если указанный угол является тупым.

Обозначим через d_k диаметр элементарной поверхности (Δ&sigma_k), .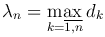

Определение. Поверхностным интегралом второго рода от функции R(x,y,z) называется предел интегральной суммы T_n при λ,sub>n→0, где λ_n - наибольший из диаметров элементарных областей.

По определению

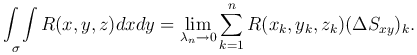
Утверждение. Если двусторонняя поверхность σ является гладкой и функция R(x,y,z) непрерывна на ней, то предел интегральной суммы T_n существует, он не зависит от способа разбиения поверхности σ на элементарные части (Δ&sigma_k) и выбора точек M_k∈(Δσ_k).

Аналогичным образом определяются поверхностные интегралы второго рода:

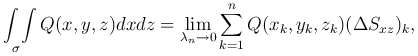
где (ΔS_xz)_k - величина проекции (Δ&sigma_k) на плоскость Oxz;

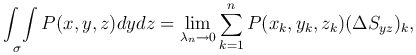
где (ΔS_xz)_k - величина проекции (Δ&sigma_k) на плоскость Oyz; а также поверхностный интеграл общего вида:

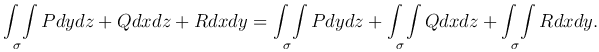
Вычисление интегралов по поверхности

Пусть требуется вычислить поверхностный интеграл первого рода

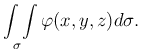
Здесь σ - гладкая поверхность, заданная уравнением

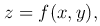
где f(x,y,z) - дифференцируемая функция.

Предположим, что поверхность σ однозначно проектируется на плоскость Oxy и S - ее проекция на эту плоскость.

По определению

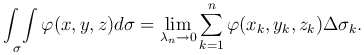
Преобразуем эту интегральную сумму. Запишем уравнение поверхности в виде F(x,y,z)=0, где F(x,y,z)=z-f(x,y). Вектор нормали n к этой поверхности имеет координаты

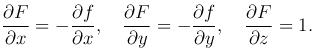
Введем обозначения:

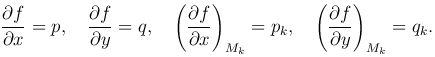
Направляющие косинусы нормали n к поверхности z-f(x,y)=0 выразятся формулами:

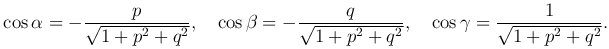
Поскольку Δσ_kcos γ_k=(ΔS_xy)_k, то

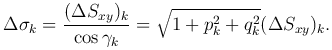
Следовательно, интегральная сумма примет вид

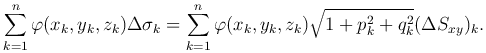
Переходя к пределу при λ_n→0, получим

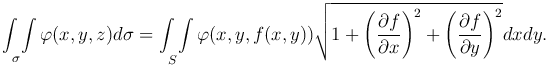
Таким образом, вычисление поверхностного интеграла первого рода свелось к вычислению соответствующего двойного интеграла по области S - проекции поверхности σ на плоскость Oxy.

Если гладкая поверхность σ задана уравнением y=f(x,z) и S₁ - ее проекция на плоскость Oxz, то

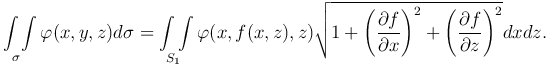
Если гладкая поверхность σ задана уравнением x=f(y,z) и S₂ - ее проекция на плоскость Oyz, то

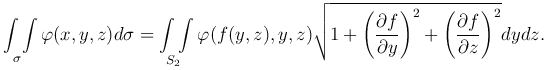
Пусть требуется вычислить поверхностный интеграл второго рода

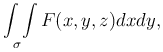
где σ - гладкая поверхность, заданная уравнением z=f(x,y).

Предположим, что σ взаимно-однозначно проектируется на область S плоскости Oxy. По определению

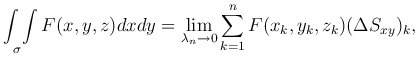
где (ΔS_xz)_k - величина проекции элементарной области (Δσ_k) на плоскость Oxy. Так как

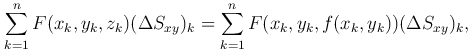
то переходя к пределу при λ_n→0, получим

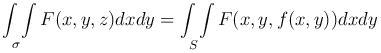
для верхней стороны поверхности, т.е. когда cos γ>0 (γ - угол между нормалью к поверхности и осью Oz);

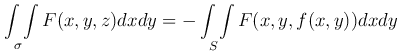
для нижней стороны поверхности, т.е. когда cos γ<0.

Аналогично вычисляются поверхностные интегралы второго рода по координатам x, y и z.