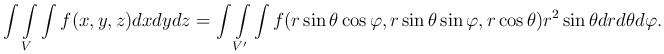Тройной интеграл

Рассмотрим ограниченную замкнутую пространственную область V и определенную в ней непрерывную функцию u=f(x,y,z). Область V разобьем на n элементарных пространственных областей ΔV₁, ΔV₂, …, ΔV_n. Предполагается, что область V и элементарные области ΔV₁, ΔV₂, …, ΔV_n имеют объемы, которые будем обозначать соответственно теми же символами. В каждой элементарной области ΔV_k (k=1,…,n) выберем произвольную точку M_k(x_k,y_k,z_k), значение функции в этой точке f(x_k,y_k,z_k) умножим на объем элементарной области ΔV_k и составим сумму всех таким произведение:

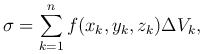
которая называется интегральной суммой данной функции по данному объему.

Обозначим через d_k диаметр области ΔV_k. Пусть λ - наибольший из этих диаметров. Рассмотрим предел интегральной суммы σ_n при λ_n→0. Если предел интегральной суммы существует, то он и называется тройным интегралом от функции f(x,y,z) по пространственной области V.

Таким образом, по определению:

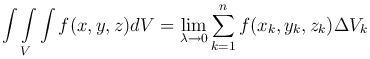
или

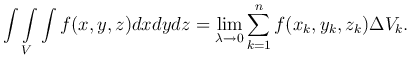
Утверждение. Если функция f(x,y,z) непрерывна в рассматриваемой замкнутой области V, то предел в правой части существует и не зависит от способа разбиения области V на элементарные и выбора точки точки M_k в элементарной области ΔV_k.

Предполагаем, что в области V распределено вещество, объемная плотность которого выражается непрерывной функцией f(x,y,z)≥0, тогда произведение f(x_k,y_k,z_k)ΔV_k выражает приближенную массу элементарной области ΔV_k, интегральная сумма σ_n - приближенную массу всей области V, а тройной интеграл - точное значение этой массы, т.е.

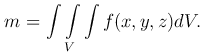
Данная формула выражает механический смысл тройного интеграла: тройной интеграл представляет массу, заполняющую область интегрирования V.

Если в последней формуле f(x,y,z)≡1, то m=V·1=V и она примет вид:

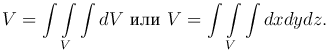
Тройной интеграл обладает свойствами, аналогичными свойствам двойного интеграла.

Вычисление тройного интеграла в прямоугольных декартовых координатах

Предположим, что область V является стандартной в направлении оси Oz, т.е. удовлетворяющей следующим условиям:

1) всякая прямая, параллельная этой оси и имеющая с данной областью общие точки, пересекает границу области только в двух точках;
2) проекция S области V на плоскость Oxy представляет собой стандартную область в направлении оси Ox или Oy.

Пусть стандартная область V ограничена сверху поверхностью z=z₂(x,y), снизу - поверхностью z=z₁(x,y), тогда можно показать, что

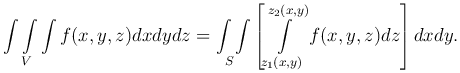
Если область S является стандартной в направлении оси Oy и определяется неравенствами a≤x≤b,

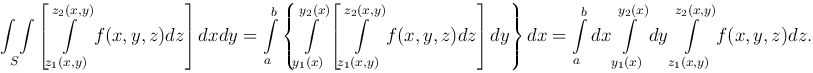
Таким образом, получаем

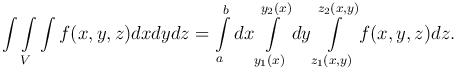
Частный случай этой формулы: если V - прямоугольный параллелепипед, определяемый неравенствами a≤x≤A, b≤y≤B, c≤z≤C, то

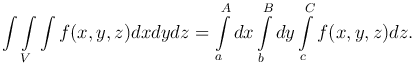
Замечание. Если S является стандартной в направлении оси Ox и определяется неравенствами x₁(y)≤x≤x₂(y), c≤y≤d, то

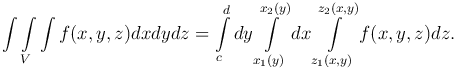
Таким образом,

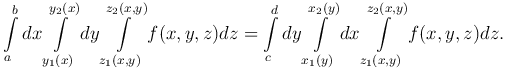
Замена переменных в тройном интеграле

Пусть в области V заданы дифференцируемые функции

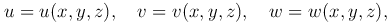
где (x,y,z) - прямоугольные декартовы координаты точки M(x,y,z)∈V.

Пусть эти уравнения однозначно разрешимы относительно x,y,z:

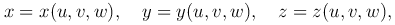
причем эти функции дифференцируемы относительно своих аргументов.

Любой точке M(x,y,z)∈V ставится в соответствие точка M'(u,v,w)∈V'; (u,v,w) называются криволинейными координатами точки M.

Функции x(u,v,w), y(u,v,w), z(u,v,w) осуществляют взаимно-однозначное отображение области V на область V'.

По аналогии с двойным интегралом получаем формулу, по которой осуществляется замена переменных:

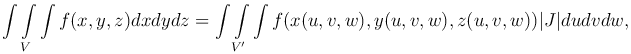
где

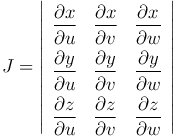
Этот определитель называется функциональным определителем или якобианом функций x(u,v,w), y(u,v,w), z(u,v,w). Предполагается, что в рассматриваемой области J≠0.

Тройной интеграл в цилиндрических и сферических координатах

В цилиндрических координатах положим u=ρ, v=φ, w=z. Найдем якобиан:

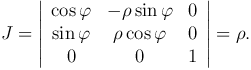
Получим

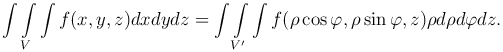
В сферических координатах положим u=r, v=θ, w=φ. Найдем якобиан:

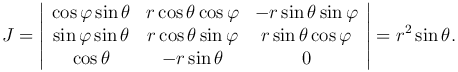
Таким образом,