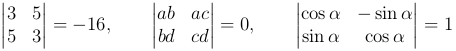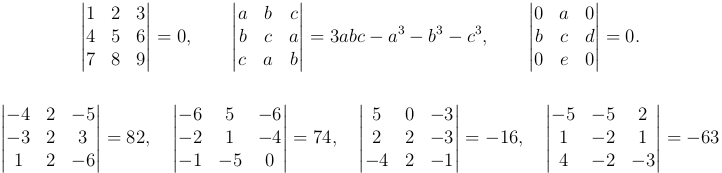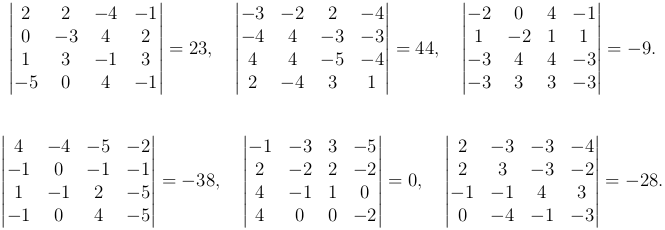Определитель

Рассмотрим квадратную матрицу второго порядка

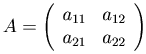
Определение. Определителем квадратной матрицы второго порядка 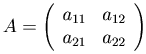называют число, равное a₁₁a₂₂-a₁₂a₂₁ и обозначают символом 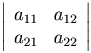, то есть

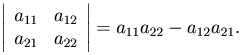
Определитель матрицы называется также детерминантом. Обозначения определителя матрицы A: |A|, Δ, det A, det(a_ij).

Теперь рассмотрим квадратную матрицу третьего порядка

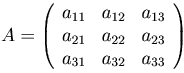
При вычислении определителя третьего порядка полезно знать правило треугольника: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположого угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольноков, построенных относительно этой диагонали. Следующая схема демонстрирует это правило. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а красным (справа) - со знаком минус.

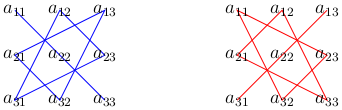
Теперь дадим определение.

Определение. Определителем квадратной матрицы третьего порядка 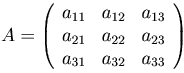называют число

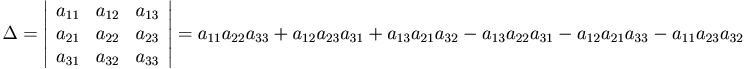
Определение. Минором какого-либо элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, к которым принадлежит данный элемент. Минор элемента a_ik обозначим M_ik.

Определение. Минор элемента a₂₁ определителя третьего порядка матрицы 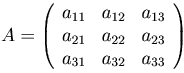является определитель второго порядка

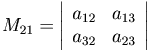
Определение. Алгебраическим дополнением элемента a_ik определителя называется его минор, взятый со знаком (-1)^i+k.

Алгебраическое дополнение элемента a_ik обозначим A_ik. По определению

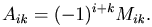
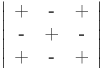
Правило для определения знака алгебраического дополнения (на примере определителя третьего порядка):

Пример. Алгебраическим дополнением элемента a₂₁ является

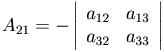
Теорема разложения. Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Свойства определителей

Определитель не изменится при замене всех его строк соответствующими столбцами.
При перестановке двух столбцов (строк) определитель меняет знак.
Определитель с двумя одинаковыми столбцами (строками) равен нулю.
Множитель, общий для элементов некоторого столбца (строки), можно выносить за знак определителя.
Определитель с двумя пропорциональными столбцами (строками) равен нулю.
Определитель равен нулю, если все элементы некоторого столбца (строки) равны нулю.
Определитель не изменится, если к элементам некоторого столбца (строки) прибавить соответствующие элементы другого столбца (строки), предварительно умножив их на один и тот же множитель.

Замечание. Если в определителе все элементы некоторого столбца (строки) равны суммам двух слагаемых, то такой определитель равен сумме двух соответствующих определителей.

Например,

Определители n-го порядка

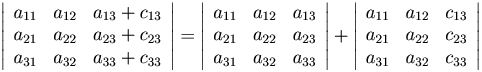
Рассмотрим квадратную матрицу n-го порядка

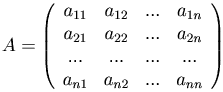
Понятие определителя этой матрицы или определителя n-го порядка вводится индуктивно, считая, что уже введено понятие определителя порядка n-1, соответствующего квадратной матрице (n-1)-го порядка.

Определение минора элемента матрицы и его алгебраического дополнения верны для определителей любого порядка.

Определение. Определителем порядка n, соответствующим матрице A n-го порядка, называют число, равное 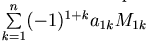(M_1k - минор элемента a_1k) и обозначаемое одним из символов

Итак, по определению

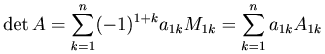
Эта формула выражает правило составления определителя порядка n по элементам первой строки соответствующей ему матрицы и по алгебраическим дополнениям этих элементов, являющимся определителем порядка n-1, взятыми с надлежащими знаками.

Для определителя любого порядка верны все свойства и теоремы, полученные и доказанные для определителя третьего порядка.

Сформулируем основную теорему:

Теорема [Теорема замещения]. Каков бы ни был номер строки i (i=1,2,…,n), для определителя n-го порядка справедлива формула

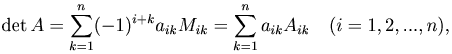
называемая разложением этого определителя по i-й строке.

Поскольку верно свойство 1 определителей, то определитель также можем разложить и по столбцу:

Примеры

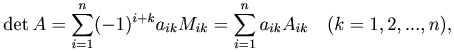
Вычислим следующий определитель:

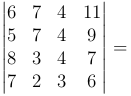
Вычтем вторую строку из первой и третьей. После прибавим к третей первую и из третей вынесем общий множитель:

Теперь ко второй строке прибавим третью, умноженную на 7, и к четвертой прибавим третью, умноженную на 2. После вынесем общий множитель из четвертой строки:

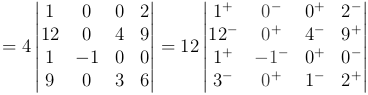
Разложим определитель по второму столбцу (знаки указывают значение (-1)^i+j при миноре). Заметим, что в столбце только один ненулевой элемент, следовательно, в разложении останется только один определитель третьего порядка. Окончательно пулучаем ответ использую формулу для определителя третьего порядка.

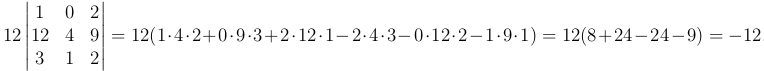
Приведем еще несколько примеров для определителей различных порядков: